a) Tập xác định:\(D = \mathbb{R}\),
* Chiều biến thiên:
+) \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \)
+) \(y' = \dfrac{3}{4}{x^2} - 3x\); \(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 4}\end{array}} \right.\)
Hàm số đồng biến trên mỗi khoảng \(( - \infty ;0),(4; + \infty )\).
Hàm số nghịch biến trên khoảng \(\left( {0;4} \right)\).
Hàm số đạt cực đại tại \(x = 0,{y_{CD}} = 5\). Hàm số đạt cực tiểu tại \(x = 4,{y_{CT}} = - 3\).
Bảng biên thiên:
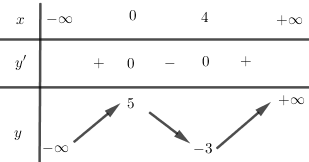
* Đồ thị:
+) Đồ thị đi qua các điểm \(A\left( { - 2; - 3} \right);B\left( {6;5} \right)\) và cắt trục \(Oy\) tại điểm \(\left( {0;5} \right)\).
+) \(y'' = \dfrac{3}{2}x - 3 = 0\) \( \Leftrightarrow x = 2 \Rightarrow y = 1\) suy ra điểm uốn \(U\left( {2;1} \right)\).
+) Vẽ đồ thị:
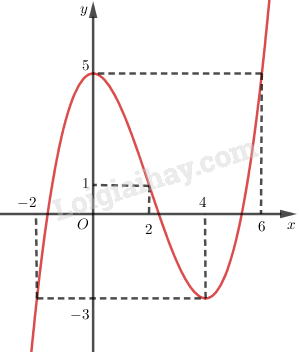
b)
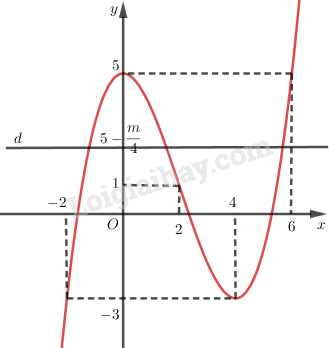
\({x^3} - 6{x^2} + m = 0\) (1)
\( \Leftrightarrow {x^3} - 6{x^2} = - m\)\( \Leftrightarrow \dfrac{1}{4}{x^3} - \dfrac{3}{2}{x^2} + 5 = 5 - \dfrac{m}{4}\)
Số nghiệm thực phân biệt của phương trình (1) bằng số giao điểm phân biệt của đồ thị \(\left( C \right)\) và đường thẳng \(\left( d \right):\)\(y = 5 - \dfrac{m}{4}\)
Suy ra \(\left( 1 \right)\) có \(3\) nghiệm thực phân biệt khi và chỉ khi \( - 3 < 5 - \dfrac{m}{4} < 5 \Leftrightarrow 0 < m < 32\).