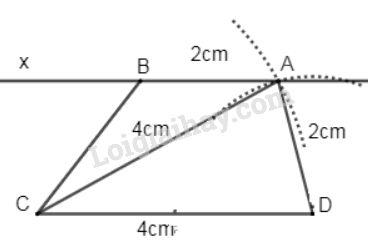
Bài 31 trang 83 SGK Toán 8 tập 1
Lời giải
Bài Tập và lời giải
II. Em suy nghĩ - Bài 18: Quyền được bảo đảm an toàn và bí mật thư tín, điện thoại, điện tín
Giải bài tập 1, 2, 3, 4 trang 39 sách bài tập tình huống Giáo dục công dân 6. Biết là thư của chồng gửi cho con, nhưng mẹ An vẫn không bóc ra xem? Vì sao?
III. Bài học rút ra - Bài 18: Quyền được bảo đảm an toàn và bí mật thư tín, điện thoại, điện tín
Em hãy rút ra bài học về đạo đức, ý thức công dân và ghi vào vở
Kể lại một câu chuyện cảm động về tình bạn mà em đã chứng kiến
Hà mải nhìn theo màu áo của Mai và nói thầm trong bụng: “Mai ơi! Thế là từ đây chúng ta mãi mãi xa nhau rồi”. Hà bước trên con đường làng quen thuộc.