
\(a)\) Chứng minh thuận:
Ta có: \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Suy ra: \(\widehat {BCD} = 90^\circ \)
\(CD = CB (gt)\)
Suy ra: \(∆BCD\) vuông cân tại \(C.\)
\( \Rightarrow \widehat {CDB} = 45^\circ \) hay \(\widehat {ADB} = 45^\circ \)
\(AB\) cố định. Khi \(C\) chuyển động trên nửa đường tròn đường kính \(AB\) thì \(D\) chuyển động trên cung chứa góc \(45^\circ \) dựng trên đoạn thẳng \(AB\) cố định.
Ta có dây \(AC\) thay đổi phụ thuộc vào vị trí điểm \(C\) trên nửa đường tròn đường kính \(AB.\)
− Dây \(AC\) lớn nhất bằng đường kính của đường tròn. Khi \(C\) trùng với \(B\) khi đó \(D\) trùng với \(B.\) Vậy \(B\) là điểm của quỹ tích.
− Dây \(AC\) nhỏ nhất có độ dài bằng \(0\) khi \(C\) trùng với \(A,\) thì khi đó \(D\) trùng với \(B’\) là giao điểm của tiếp tuyến đường tròn đường kính \(AB\) tại \(A\) với cung chứa góc \(45^\circ\) vẽ trên \(AB.\)
Chứng minh đảo:
Lấy điểm \(D’\) tùy ý trên cung \(BB’,\) nối \(AD’\) cắt đường tròn đường kính \(AB\) tại \(C’.\) Nối \(BC’, BD’.\)
Ta có: \(\widehat {AD'B} = 45^\circ \) (vì \(D’\) nằm trên cung chứa góc \(45^\circ\) vẽ trên \(AB\)).
Trong đường tròn đường kính \(AB\) ta có:
\(\widehat {AC'B} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \widehat {BC'D'} = 90^\circ \)
Suy ra: \(∆BC’D’\) vuông cân tại \(C’\)
\( \Rightarrow C’B = C’D’\)
Vậy quỹ tích các điểm \(D\) khi \(C\) chuyển động trên nửa đường tròn đường kính \(AB\) là cung \(\overparen{BB'}\) nằm trên cung chứa góc \(45^\circ\) vẽ trên đoạn \(AB,\) trong nửa mặt phẳng bờ \(AB\) có chứa điểm \(C.\)
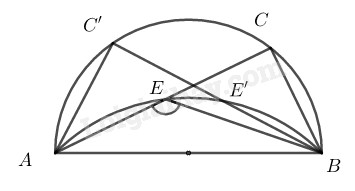
\(b)\) Chứng minh thuận:
Trong đường tròn đường kính \(AB\) ta có:
\(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
\(CB = CE (gt)\)
\( \Rightarrow ∆CBE\) vuông tại \(C\)
\( \Rightarrow \widehat {CEB} = 45^\circ \)
\(\widehat {CEB} + \widehat {AEB} = 180^\circ \) (hai góc kề bù)
\( \Rightarrow \widehat {AEB} = 135^\circ \)
\(AB\) cố định, \(C\) chuyển động trên đường tròn đường kính \(AB\) thì \(E\) chuyển động trên cung chứa góc \(135^\circ\) dựng trên đoạn \(AB\) cố định.
− Khi dây \(AC\) có độ dài lớn nhất bằng đường kính đường tròn, thì \(C\) trùng với \(B\) nên \(E\) trùng với \(B\) \( \Rightarrow \) \(B\) là \(1\) điểm của quỹ tích.
− Khi dây \(AC\) có độ dài nhỏ nhất bằng \(0\) thì \(C\) trùng với \(A.\) Khi đó \(E\) trùng \(A\) nên \(A\) là \(1\) điểm của quỹ tích.
Vậy \(E\) chuyển động trên \(1\) cung chứa góc \(135^\circ\) vẽ trên đoạn \(AB\) nằm trên nửa mặt phẳng bờ \(AB\) chứa điểm \(C.\)
Chứng minh đảo:
Lấy \(E’\) bất kỳ trên cung chứa góc \(135^\circ .\) Kẻ \(AE’\) cắt đường tròn đường kính \(AB\) tại \(C’.\) Nối \(BE’, BC’.\)
Ta có: \(\widehat {AE'B} = 135^\circ \) (vì \(E’\) nằm trên cung chứa góc \(135^\circ\))
\(\widehat {AE'B} + \widehat {BE'C} = 180^\circ \) (kề bù)
\( \Rightarrow \widehat {BE'C'} = 180^\circ - \widehat {AE'B} \)\(= 180^\circ - 135^\circ = 45^\circ \)
Trong đường tròn đường kính \(AB\) ta có:
\(\widehat {AC'B} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Suy ra: \(∆E’C’B\) vuông cân tại \(C’.\)
\( \Rightarrow C'E' = C'B\)
Vậy quỹ tích các điểm \(E\) khi \(C\) chuyển động trên đường tròn đường kính \(AB\) là một cung chứa góc \(135^\circ\) vẽ trên đoạn \(AB\) nằm trên nửa mặt phẳng bờ \(AB\) chứa điểm \(C.\)