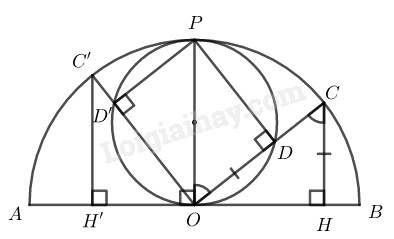
Chứng minh thuận:
Từ \(O\) kẻ đường thẳng vuông góc với \(AB\) cắt nửa đường tròn đường kính \(AB\) tại \(P.\) \(O\) cố định, đường tròn đường kính \(AB\) cố định suy ra \(P\) cố định.
Nối \(PD.\) Ta có: \(OP // CH\) (vì hai đường thẳng cùng vuông góc với \(AB\))
Xét \(∆OCH\) và \(∆OPD\) có:
\(OD = CH (gt)\)
\(OP = OC\) (bán kính)
\(\widehat {POD} = \widehat {OCH}\) (so le trong)
Suy ra: \(∆DOP = ∆HCO (c.g.c)\)
\( \Rightarrow \)\(\widehat {ODP} = \widehat {CHO}\) mà \(\widehat {CHO} = 90^\circ \) nên \(\widehat {ODP} = 90^\circ \)
Khi \(C \) chuyển động trên nửa đường tròn đường kính \(AB\) thì \(D\) thay đổi tạo với \(2\) đầu đoạn thẳng \(OP\) cố định một góc \(\widehat {OPD} = 90^\circ \). Vậy \(D\) chuyển động trên đường tròn đường kính \(OP.\)
Chứng minh đảo:
Lấy điểm \(D'\) bất kỳ trên đường tròn đường kính \(OP.\) Kẻ \(OD'\) cắt nửa đường tròn đường kính \(AB\) tại \(C',\) kẻ \(C'H'⊥ AB\) ta phải chứng minh \(OD' = C'H'.\)
Nối \(PD'.\)
Xét \(∆C'H'O\) và \(∆PD'O\) có:
+) \(\widehat {C'H'O} = \widehat {PD'O} = 90^\circ \)
+) \(OC' = OP\) (bán kính đường tròn tâm \(O\))
+) \(\widehat {D'OP} = \widehat {OC'H'}\) (so le trong)
Suy ra: \(∆C'H'O = ∆PD'O\) (cạnh huyền, góc nhọn)
\( \Rightarrow C'H' = OD'\)
Vậy quỹ tích các điểm \(D\) khi \(C\) chuyển động trên nửa đường tròn đường kính \(AB\) là đường tròn đường kính \(OP.\)