Phân tích:
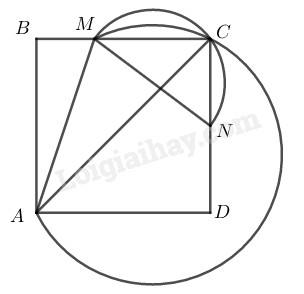
Giả sử hình vuông \(ABCD\) dựng được thỏa mãn điều kiện bài toán. Ta cần dựng đỉnh \(C.\) Đỉnh \(C\) thỏa mãn \(2\) điều kiện:
− \(\widehat {MCN} = 90^\circ \) nên \(C\) nằm trên cung chứa góc \(90^\circ\) dựng trên \(MN.\)
− Ta có \(\widehat {ACM} = 45^\circ \) (vì hình vuông có đường chéo là phân giác) nên \(C\) nằm trên cung chứa góc \(45^\circ\) vẽ trên \(AM.\)
Cách dựng:
− Dựng cung chứa góc \(90^\circ\) trên đoạn \(MN.\)
− Dựng cung chứa góc \(45^\circ\) trên đoạn \(AM.\)
Hai cung cắt nhau tại \(C,\) nối \(CM, CN.\)
Kẻ \(AB ⊥ CN\) tại \(B, AD ⊥ CN\) tại \(D.\)
Ta có tứ giác \(ABCD\) là hình vuông cần dựng.
Chứng minh: Thật vậy theo cách dựng ta có: \(\widehat C = 90^\circ ,\widehat B = 90^\circ ,\widehat D = 90^\circ \)
Tứ giác \(ABCD\) là hình chữ nhật, có điểm \(M\) thuộc \(BC,\) điểm \(N\) thuộc \(CD.\) \(AC\) là phân giác của \(\widehat C.\)
Vậy: tứ giác \(ABCD\) là hình vuông.