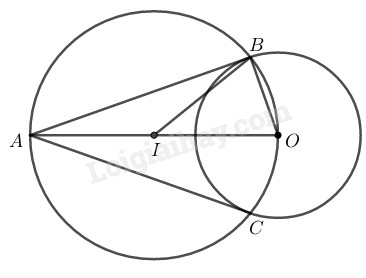
* Phân tích
Giả sử tiếp tuyến \(AB\) và \(AC\) cần dựng thỏa mãn điều kiện bài toán.
Ta có: \(AB ⊥ OB\) \(\widehat {ABO} = 90^\circ \)
\(AC \bot OC \Rightarrow \widehat {ACO} = 90^\circ \)
Tam giác \(ABO\) có \(\widehat {ABO} = 90^\circ \) nội tiếp trong đường tròn đường kính \(AO\) và tam giác \(ACO\) có \(\widehat {ACO} = 90^\circ \) nội tiếp trong đường tròn đường kính \(AO.\)
Suy ra \(B\) và \(C\) là giao điểm của đường tròn đường kính \(AO\) với đường tròn \((O).\)
* Cách dựng
− Dựng \(I\) là trung điểm của \(OA.\)
− Dựng đường tròn \(( I; IO)\) cắt đường tròn \((O)\) tại \(B\) và \(C.\)
− Nối \(AB, AC\) ta được hai tiếp tuyến cần dựng.
* Chứng minh
Tam giác \(ABO\) nội tiếp trong đường tròn \((I)\) có \(OA\) là đường kính nên: \(\widehat {ABO} = 90^\circ \)
Suy ra: \(AB ⊥ OB\) tại \(B\) nên \(AB\) là tiếp tuyến của đường tròn \((O).\)
Tam giác \(ACO\) nội tiếp trong đường tròn \((I)\) có \(OA\) là đường kính nên : \(\widehat {ACO} = 90^\circ \)
Suy ra: \(AC ⊥ OC\) tại \(C\) nên \(AC\) là tiếp tuyến của đường tròn \((O)\)
* Biện luận
Luôn dựng được đường tròn tâm \(I,\) cắt đường tròn tâm \(O\) tại hai điểm \(B\) và \(C\) và luôn có \(AB, AC\) là hai tiếp tuyến của đường tròn \((O).\)