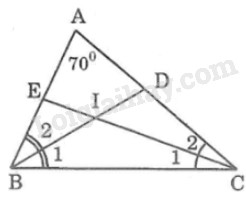
Trong \(∆ABC\) ta có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong tam giác)
\( \Rightarrow \widehat B + \widehat C = 180^\circ - \widehat A \)\(= 180^\circ - 70^\circ\, = 110^\circ \)
Lại có:
\(\widehat {{B_1}} = \dfrac{1 }{ 2}\widehat B\) (vì \(BD\) là tia phân giác góc \(B)\)
\(\widehat {{C_1}} = \dfrac{1 }{2}\widehat C\) (vì \(CE\) là tia phân giác góc \(C)\)
Trong \(∆BIC\) ta có:
\(\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \) (tổng 3 góc trong tam giác)
\(\Rightarrow \widehat {BIC} = 180 - (\widehat {{B_1}} + \widehat {{C_1}})\)
\(\widehat {BIC} = 180^\circ - \dfrac{1}{2}(\widehat B + \widehat C) \)\(\,= 180^\circ - \dfrac{1 }{ 2}.110^\circ = 125^\circ \)