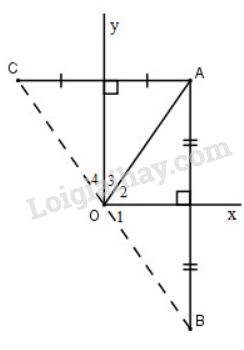
\(A\) đối xứng với \(B\) qua \(Ox\) (giả thiết) nên \(Ox\) là đường trung trực của \(AB\)
\( \Rightarrow \) \(OA = OB\) (tính chất đường trung trực của đoạn thẳng) (1)
\(\Rightarrow \Delta AOB\) cân tại \(O\) (dấu hiệu nhận biết tam giác cân)
Do đó \(Ox\) vừa là đường trung trực đồng thời là phân giác của \( \Delta AOB\)
\( \Rightarrow \) \(\widehat O_1=\widehat O_2\) (3)
\(A\) đối xứng với \(C\) qua \(Oy\) (giả thiết) nên \(Oy\) là đường trung trực của \(AC\)
\( \Rightarrow \) \(OA = OC\) (tính chất đường trung trực của đoạn thẳng) (2)
\(\Rightarrow \Delta AOC\) cân tại \(O\) (dấu hiệu nhận biết tam giác cân)
Do đó \(Oy\) vừa là đường trung trực đồng thời là phân giác của \( \Delta AOC\)
\( \Rightarrow \) \(\widehat O_3=\widehat O_4\) (4)
Từ (1) và (2) \( \Rightarrow \) \(OB = OC\) (*)
Từ (3) và (4) \( \Rightarrow \) \(\widehat O_1+\widehat O_2+\widehat O_3+\widehat O_4\)\(=2(\widehat O_2+\widehat O_3)=2.90^0=180^0\)
Do đó \(B, O, C\) thẳng hàng (2*)
Từ (*) và (2*) \( \Rightarrow \) \(B\) đối xứng với \(C\) qua \(O\).