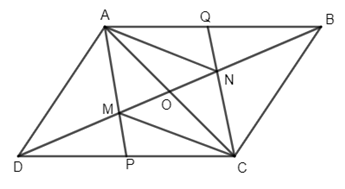
a) Ta có: OB = OD (tính chất hai đường chéo của hình bình hành)
BN = DM (gt)
\( \Rightarrow OB - BN = OD - DM\)
\( \Rightarrow ON = OM\) hay O là trung điểm MN chứng tỏ M và N đối xứng nhau qua O.
b) Tứ giác ANCM có OM = ON (cmt)
OA = OC (gt)
\( \Rightarrow ANCM\) là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường) \( \Rightarrow AM// CN\) hay \(AP// CQ\) lại có \(AQ//CP.\) Do đó AQCP là hình bình hành (các cạnh đối song song) mà O là trung điểm của đường chéo AC nên đường chéo thứ hai PQ phải qua O hay OP = OQ.
Chứng tỏ P và Q đối xứng nhau qua O.