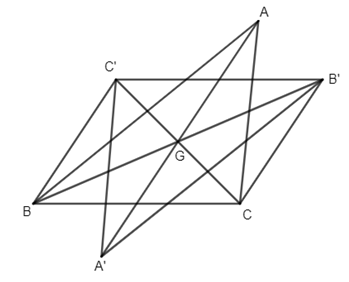
a) \(B’ B\) và \(C’,C\) đối xứng nhau qua G nên G là trung điểm của \(BB’\) và \(CC’\)
\( \Rightarrow BC’B’C\) là hình bình hành.
b) Chứng minh tương tự ta được \(AB’,A’B,C’ACA’\) là hình bình hành
suy ra
\(\eqalign & B’C’= BC, \)
\( C’A’ = AC,\)
\( B’A’ = AB \)
Do đó \(\Delta A’B’C’= \Delta ABC\left( {c.c.c} \right)\)