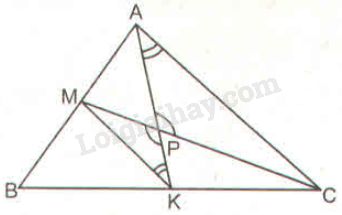
\(AP = 2 PK\) và \(CP = 2PM\) (gt)
\( \Rightarrow \displaystyle{{PK} \over {PA}} = {1 \over 2};{{PM} \over {PC}} = {1 \over 2}\)
\( \Rightarrow\displaystyle {{PK} \over {PA}} = {{PM} \over {PC}} = {1 \over 2}\)
Xét \(∆ PKM\) và \(∆ PAC\) có:
\(\displaystyle {{PK} \over {PA}} = {{PM} \over {PC}}\) (chứng minh trên)
\(\widehat {APC} = \widehat {KPM}\) (đối đỉnh)
\( \Rightarrow ∆ PKM\) đồng dạng \(∆ PAC\) (c.g.c) với tỉ số đồng dạng \(k =\displaystyle {{PK} \over {PA}}= {1 \over 2}\).
\( \Rightarrow\displaystyle {{KM} \over {AC}} = {1 \over 2}\) (1)
Vì \(∆ PKM\) đồng dạng \(∆ PAC\) suy ra \(\widehat {PKM} = \widehat {PAC}\)
Mà \(\widehat {PKM} \) và \( \widehat {PAC}\) ở vị trí so le trong nên \( KM // AC\) (vì có cặp góc ở vị trí so le trong bằng nhau).
Trong tam giác \(ABC\) có \(KM // AC\) nên \( ∆ BMK\) đồng dạng \(∆ BAC\) (g.g)
\( \Rightarrow\displaystyle {{BM} \over {BA}} = {{BK} \over {BC}} = {{MK} \over {AC}}\) (2)
Từ (1) và (2) suy ra: \(\displaystyle {{BM} \over {BA}} = {{BK} \over {BC}} = {1 \over 2}\)
Do đó \(BM = \displaystyle {1 \over 2} BA\) nên \(M\) là trung điểm của \(AB\).
\(BK =\displaystyle {1 \over 2} BC\) nên \(K\) là trung điểm của \(BC\).
Vậy \(AK\) và \(CM\) là đường trung tuyến của tam giác \(ABC.\)