* Trường hợp \(\widehat B\) nhọn:
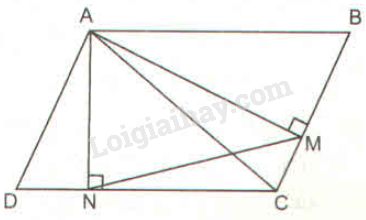
Xét \(∆ AMB\) và \(∆ AND\) có:
\(\widehat {AMB} = \widehat {AND} = 90^\circ \)
\(\widehat B = \widehat D\) (vì \(ABCD\) là hình bình hành)
\( \Rightarrow ∆ AMB\) đồng dạng \(∆ AND\) (g.g)
\( \displaystyle \Rightarrow {{AM} \over {AB}} = {{AN} \over {AD}} \)
Mà \(AD = BC\) (vì \(ABCD\) là hình bình hành)
\( \displaystyle \Rightarrow {{AM} \over {AB}} = {{AN} \over {BC}}\)
Lại có: \(AB // CD\) (gt)
\(AN ⊥ CD\) (gt)
\(\Rightarrow AN ⊥ AB\) hay \(\widehat {NAB} = {90^o}\).
\(\Rightarrow \widehat {NAM} + \widehat {MAB} = 90^\circ \) (1)
Trong tam giác vuông \(AMB\) có \(\widehat {AMB} = 90^\circ \)
\(\Rightarrow \widehat {MAB} + \widehat B = 90^\circ \) (2)
Từ (1) và (2) suy ra: \(\widehat {NAM} = \widehat B\)
Xét \(∆ ABC\) và \(∆ MAN\) có:
\( \displaystyle{{AM} \over {AB}} = {{AN} \over {BC}}\) (chứng minh trên)
\(\widehat {NAM} = \widehat B\) (chứng minh trên)
\(\Rightarrow ∆ ABC\) đồng dạng \(∆ MAN \) (c.g.c)
* Trường hợp \(\widehat B\) tù:
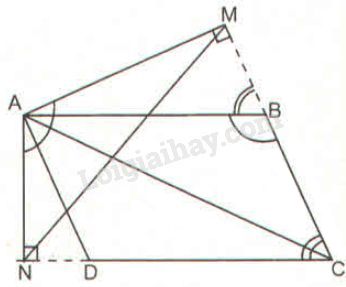
\(ABCD\) là hình bình hành nên \(AB//CD;\;AD//BC\).
Vì \(AB//CD\) nên \(\widehat {ABM} =\widehat C\) (cặp góc đồng vị).
Vì \(AD//BC\) nên \(\widehat {ADN}=\widehat C\) (cặp góc đồng vị).
Xét \(∆ AMB\) và \(∆ AND\) có:
\(\widehat {AMB} = \widehat {AND} = 90^\circ \)
\(\widehat {ABM} = \widehat {ADN}\) (vì cùng bằng \(\widehat C\))
\(\Rightarrow ∆ AMB\) đồng dạng \(∆ AND\) (g.g)
\( \displaystyle \Rightarrow {{AM} \over {AB}} = {{AN} \over {AD}}\)
Mà \(AD = BC\) (vì \(ABCD\) là hình bình hành)
\( \displaystyle \Rightarrow{{AM} \over {AB}} = {{AN} \over {BC}}\)
Vì \(AB // CD\) nên \(\widehat {ABC} + \widehat C = 180^\circ \) (cặp góc trong cùng phía) (3)
Tứ giác \(AMCN\) có \(\widehat {AMC} = \widehat {AND} = 90^\circ \)
\(\Rightarrow \widehat {MAN} + \widehat C = 180^\circ \) (4)
Từ (3) và (4) suy ra \(\widehat {MAN} = \widehat {ABC}\)
Xét \(∆ MAN\) và \(∆ ABC\) có:
\( \displaystyle {{AM} \over {AB}} = {{AN} \over {BC}}\) (chứng minh trên)
\(\widehat {MAN} = \widehat {ABC}\) (chứng minh trên)
\(\Rightarrow ∆ MAN\) đồng dạng \(∆ ABC\) (c.g.c)