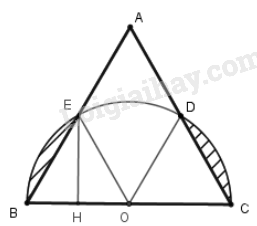
Gọi \(D,E\) lần lượt là giao của hai cạnh \(AB,AC\) với nửa đường tròn đường kính \(BC\) có tâm \(O\) là trung điểm \(BC.\)
Bán kính nửa đường tròn này là \(R = \dfrac{{BC}}{2} = \dfrac{a}{2}\)
Nối \(OE;OD.\) Xét tam giác \(OBE\) có \(OE = OB = R = \dfrac{{BC}}{2} = \dfrac{a}{2}\) và \(\widehat B = 60^\circ \Rightarrow \Delta OBE\) là tam giác đều cạnh \(\dfrac{a}{2}\)
Tương tự ta có \(\Delta OCD\) đều cạnh \(\dfrac{a}{2}.\)
+ Diện tích hình viên phân thứ nhất là \({S_1} = {S_{qBOE}} - {S_{\Delta BOE}}\)
Diện tích hình quạt \(BOE\) có bán kính \(R = OB = \dfrac{a}{2}\) và số đo cung \(BE = \widehat {BOE} = 60^\circ \) là \({S_{qBOE}} = \dfrac{{\pi {R^2}n}}{{360}} = \dfrac{{\pi {{\left( {\dfrac{a}{2}} \right)}^2}.60}}{{360}} = \dfrac{{\pi {a^2}}}{{24}}\)
Kẻ \(EH \bot OB\) tại \(H\) suy ra \(H\) là trung điểm của \(OB\) (vì tam giác \(OEB\) đều nên \(EH\) vừa là đường cao vừa là đường trung tuyến). Suy ra \(OH = \dfrac{{OB}}{2} = \dfrac{{\dfrac{a}{2}}}{2} = \dfrac{a}{4}.\)
Xét tam giác \(EHO\) vuông tại \(H,\) theo định lý Pytago ta có \[EH = \sqrt {E{O^2} - O{H^2}} = \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} - {{\left( {\dfrac{a}{4}} \right)}^2}} = \dfrac{{\sqrt 3 }}{4}a\]
Diện tích tam giác \(EOB\) là \({S_{\Delta BOE}} = \dfrac{1}{2}EH.OB = \dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{4}.\dfrac{a}{2} = \dfrac{{{a^2}\sqrt 3 }}{{16}}\)
Từ đó diện tích hình viên phân thứ nhất là \({S_1} = {S_{qBOE}} - {S_{\Delta BOE}} = \dfrac{{\pi {a^2}}}{{24}} - \dfrac{{{a^2}\sqrt 3 }}{{16}} = \dfrac{{{a^2}\left( {2\pi - 3\sqrt 3 } \right)}}{{48}}\)
Tương tự ta có diện tích hình viên phân thứ nhất là \({S_2} = {S_{qDOC}} - {S_{\Delta OCD}} = \dfrac{{{a^2}\left( {2\pi - 3\sqrt 3 } \right)}}{{48}}.\)
Vậy diện tích hai hình viên phhân bên ngoài tam giác là:
\(S=S_1+S_2=\dfrac{a^{2}}{24}\left ( 2\pi -3\sqrt{3} \right ).\)