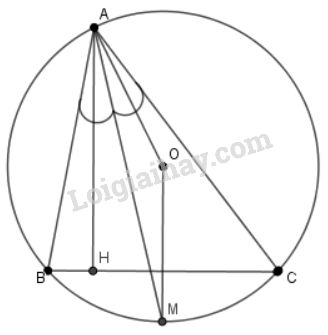
a) Vì \(AM\) là tia phân giác của \(\widehat {BAC}\) nên \(\widehat {BAM} = \widehat {MAC}\)
Mà \(\widehat {BAM}\) và \(\widehat {MAC}\) đều là góc nội tiếp của \((O)\) nên
\(\overparen{BM}\)=\(\overparen{MC}\)
⇒ \(M\) là điểm chính giữa cung \(BC\)
Vậy \(OM \bot BC\) và \(OM\) đi qua trung điểm của \(BC\)
b) Ta có : \(OM \bot BC\) và \(AH\bot BC\) nên \(AH//OM\)
\( \Rightarrow \widehat {HAM} = \widehat {AM{\rm{O}}}\) (so le trong) (1)
Mà \(∆OAM\) cân tại \(O\) nên \(\widehat {AM{\rm{O}}} = \widehat {MAO}\) (2)
Từ (1) và (2) suy ra: \(\widehat {HA{\rm{M}}} = \widehat {MAO}\)
Vậy \(AM\) là đường phân giác của góc \(OAH\)