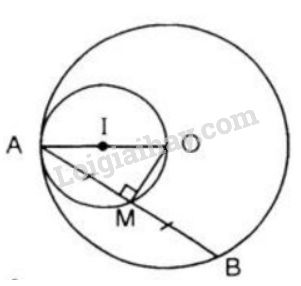
+) Phần thuận: Giả sử \(M\) là trung điểm của dây \(AB\). Do đó, \(OM \bot AB\) hay \(\widehat {AMO} = 90^\circ \). Khi \(B\) di động trên đường tròn \((O)\) điểm \(M\) luôn nhìn đoạn \(OA\) cố định dưới một góc vuông. Vậy quỹ tích của điểm \(M\) là đường tròn tâm \(I\) đường kính \(OA\).
+) Phần đảo: Lấy điểm \(M’\) bất kì trên đường tròn \((I)\). Nối \(M’\) với \(A\), đường thẳng \(M’A\) cắt đường tròn \((O)\) tại \(B’\). Nối \(M’\) với \(O\), ta có \(\widehat {AM'O} = {90^0}\) hay \(OM’ \bot AB’ \)
⇒ \(M\) là trung điểm của \(AB’\)
Kết luận: Tập hợp các trung điểm \(M\) của dây \(AB\) là đường tròn đường kính \(OA\).