Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 2 - Đại số 9

Bài 1. Cho hàm số \(y = (m – 1)x + 2\) có đồ thị là đường thẳng (d).

a. Tìm m biết (d) đi qua \(A(2; 1)\) và vẽ đồ thị với m vừa tìm được.

b. Viết phương trình đường thẳng (d’) qua \(M(1; 3)\) và cắt trục tung tại điểm có tung độ bằng 5. Tìm tọa độ giao điểm của (d) và (d’)

Bài 2. Cho hai đường thẳng : \(y = x – 1\) (d₁) và \(y = -x + 3\) (d₂)

a. Vẽ hai đường thẳng trên cùng mặt phẳng tọa độ.

b. Gọi M là giao điểm của (d₁) và (d₂). Viết phương trình đường thẳng qua M và O (O là gốc tọa độ).

c. Tính góc α tạo bởi (d₂) và trục Ox.

Bài 1. a. \(A \in \left( d \right) \Rightarrow 1 = 2\left( {m - 1} \right) + 2 \)

\(\Rightarrow m = {1 \over 2}\)

Ta có: \(y =  - {1 \over 2}x + 2\)

Đồ thị của hàm số là đường thẳng qua \(A(2; 1)\) và \(B(0; 2)\).

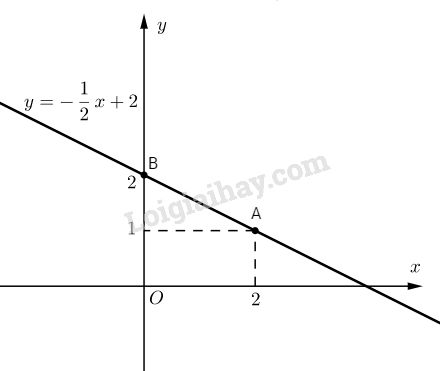
b. Phương trình (d’) có dạng: \(y = ax + b\; (a≠ 0)\)

Vì (d’) cắt Oy tại điểm có tung độ bằng 5 nên \(b = 5\)

Khi đó: \(y = ax + 5\)

\(M \in \left( {d'} \right) \Rightarrow 3 = a + 5 \Rightarrow a =  - 2\)

Vậy phương trình (d’) : \(y = -2x + 5\)

Phương trình hoành độ giao điểm của (d) và (d’):

\( - {1 \over 2}x + 2 =  - 2x + 5 \Leftrightarrow x = 2\)

Thế \(x = 2\) vào phương trình của (d’), ta được \(y = 1\).

Vậy tọa độ giao điểm là \((2; 1)\).

Bài 2. a. Đường thẳng (d₁) qua hai điểm \(A(0; -1)\) và \(B(1; 0).\)

Đường thẳng (d₂) qua hai điểm \(C(0; 3)\) và \(D(3; 0)\)

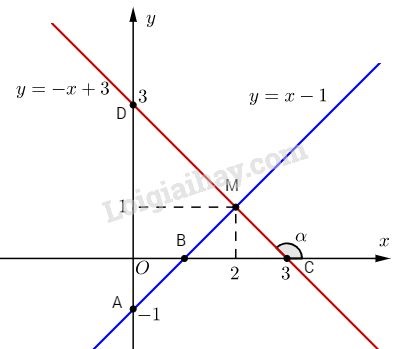
b. Phương trình hoành độ giao điểm của (d₁) và (d₂) :

\(x – 1 = -x + 3 ⇔ x = 2\)

Thế \(x = 2\) vào phương trình (d₁) \(⇒ y = 1\).

Vậy \(M(2; 1)\).

Phương trình đường thẳng qua O có dạng : \(y = ax\)

Đường thẳng này qua M \(⇒ 1 = a.2 \Rightarrow a = {1 \over 2}\)

Vậy phương trình đường thẳng OM là : \(y = {1 \over 2}x\)

c. Trong tam giác vuông OCD, ta có: \(OC = OD = 3\)

\( \Rightarrow \tan \widehat {CDO} = {3 \over 3} = 1 \Rightarrow \widehat {CDO} = 45^\circ \)

\(\Rightarrow \widehat {CDx} = 180^\circ  - 45^\circ  = 135^\circ \)

Vậy \(\alpha  = 135^\circ \)