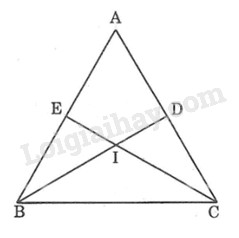
Giả sử \(∆ABC\) có hai đường trung tuyến \(BD, CE \) và \(BD = CE.\) Gọi \(G\) là giao điểm \(BD\) và \(CE.\)
\(\displaystyle BG = {2 \over 3}B{\rm{D}}\) (tính chất đường trung tuyến)
\(\displaystyle CG = {2 \over 3}CE\) (tính chất đường trung tuyến)
Mà \(BD = CE\)
Suy ra: \(BG = CG\)
\( \Rightarrow BG + GD = CG + GE\)
\( \Rightarrow GD = GE\)
Xét \(∆BGE\) và \(∆CGD:\)
+) \(BG = CG\) (chứng minh trên)
+) \(\widehat {BGE} = \widehat {CG{\rm{D}}}\) (đối đỉnh)
+) \(GE = GD\) (chứng minh trên)
Do đó: \(∆BGE = ∆CGD\) (c.g.c)
\( \Rightarrow BE = CD\) (1)
\(\displaystyle BE = {1 \over 2}AB\) (vì \(E\) là trung điểm \(AB)\) (2)
\(\displaystyle C{\rm{D = }}{1 \over 2}AC\) (vì \(D\) là trung điểm \(AC) \) (3)
Từ (1), (2) và (3) suy ra: \(AB = AD.\)
Vậy \(∆ABC\) cân tại \(A.\)