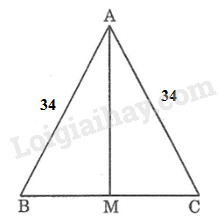
a) Xét \(∆AMB\) và \(∆AMC:\)
+) \(AB = AC\) (gt)
+) \(BM = CM \) (gt)
+) \(AM\) cạnh chung
Do đó: \(∆AMB = ∆AMC\) (c.c.c)
\( \Rightarrow \widehat {AMB} = \widehat {AMC}\) (1)
Ta có: \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (hai góc kề bù) (2)
Từ (1) và (2) suy ra: \(\widehat {AMB} = \widehat {AMC} = 90^\circ \)
Vậy: \(AM \bot BC\)
b) Xét tam giác vuông \(AMB\) ta có: \(\widehat {AMB} = 90^\circ \)
Theo định lý Pytago ta có:
\(\eqalign{
& \,\,\,\,A{B^2} = A{M^2} + B{M^2} \cr
& \Rightarrow A{M^2} = A{B^2} - B{M^2} \cr
&\Rightarrow AM^2= {34^2} - {16^2} \cr
&\Rightarrow A{M^2} = 1156 - 256 = 900 \cr
& \Rightarrow AM = 30\left( {cm} \right) \cr} \)