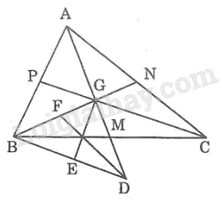
a) Gọi \(\displaystyle AM, BN, CP\) là các đường trung tuyến của \(\displaystyle ∆ABC\) cắt nhau tại \(\displaystyle G.\)
Vì \(\displaystyle AG = GD\) (gt)
Mà \(\displaystyle AG = 2GM\) (suy ra từ tính chất đường trung tuyến)
Nên \(\displaystyle GD = 2GM\)
Lại có \(\displaystyle GD = GM + MD\)
Suy ra: \(\displaystyle GM = MD\)
Xét \(\displaystyle ∆BMD\) và \(\displaystyle ∆CMG:\)
+) \(\displaystyle BM = CM\) (gt)
+) \(\displaystyle \widehat {BM{\rm{D}}} = \widehat {CMG}\) (đối đỉnh)
+) \(\displaystyle MD = GM\) (chứng minh trên)
Do đó: \(\displaystyle ∆BMD = ∆CMG\) (c.g.c)
\(\displaystyle \Rightarrow BD = CG\)
Mà \(\displaystyle CG = {2 \over 3}CP\) (tính chất đường trung tuyến)
Suy ra: \(\displaystyle B{\rm{D = }}{2 \over 3}CP\) (1)
\(\displaystyle BG = {2 \over 3}BN\) (tính chất đường trung tuyến) (2)
\(\displaystyle {\rm{A}}G = {2 \over 3}AM\) (tính chất đường trung tuyến)
Suy ra: \(\displaystyle G{\rm{D}} = {2 \over 3}AM\) (3)
Từ (1), (2) và (3) suy ra các cạnh của \(\displaystyle ∆BGD\) bằng \(\displaystyle {2 \over 3}\) các đường trung tuyến của \(\displaystyle ∆ABC.\)
b) * Vì \(\displaystyle GM = MD\) (chứng minh trên) nên \(\displaystyle BM\) là đường trung tuyến của \(\displaystyle ∆BGD\)
Suy ra \(\displaystyle BM = {1 \over 2}BC\) (4)
* Kẻ đường trung tuyến \(\displaystyle GE\) và \(\displaystyle DF\) của \(\displaystyle ∆BGD\)
\(\displaystyle \Rightarrow FG = {1 \over 2}BG\)
\(\displaystyle GN = {1 \over 2}BG\) (tính chất đường trung tuyến)
Nên \(\displaystyle FG = GN\)
Xét \(\displaystyle ∆DFG\) và \(\displaystyle ∆ANG:\)
+) \(\displaystyle AG = GD\) (gt)
+) \(\displaystyle \widehat {DGF} = \widehat {AGN}\) (đối đỉnh)
+) \(\displaystyle GF = GN\) (chứng minh trên)
Do đó \(\displaystyle ∆DFG = ∆ANG\) (c.g.c)
\(\displaystyle \Rightarrow DF = AN \)
Mà \(\displaystyle AN = {1 \over 2}AC\) (gt)
Suy ra: \(\displaystyle {\rm{D}}F = {1 \over 2}AC\) (5)
* Ta có \(\displaystyle BD = CG) (chứng minh câu a)
Mà \(\displaystyle {\rm{ED}} = {1 \over 2}B{\rm{D}}\) (vì \(\displaystyle E\) là trung điểm \(\displaystyle BD)\)
\(\displaystyle GP = {1 \over 2}CG\) (tính chất ba đường trung tuyến)
Suy ra: \(\displaystyle ED = GP\)
Lại có \(\displaystyle ∆BDM = ∆CGM\) (chứng minh trên)
\(\displaystyle \Rightarrow \widehat {B{\rm{D}}M} = \widehat {CGM}\) hay \(\displaystyle \widehat {E{\rm{D}}G} = \widehat {CGM}\)
Mà \(\displaystyle \widehat {CGM} = \widehat {PGA}\) (đối đỉnh)
Suy ra: \(\displaystyle \widehat {{\rm{ED}}G} = \widehat {PGA}\)
Lại có: \(\displaystyle AG = GD\) (gt) và \(\displaystyle ED = GP\) (cmt)
Suy ra: \(\displaystyle ∆PGA = ∆EDG\) (c.g.c)
\(\displaystyle \Rightarrow GE = AP\) mà \(\displaystyle AP = \dfrac{1}{2}AB\)
Suy ra: \(\displaystyle GE = {1 \over 2}AB\) (6)
Từ (4),(5) và (6) suy ra các đường trung tuyến của \(\displaystyle ∆BGD\) bằng một nửa cạnh của \(\displaystyle ∆ABC.\)