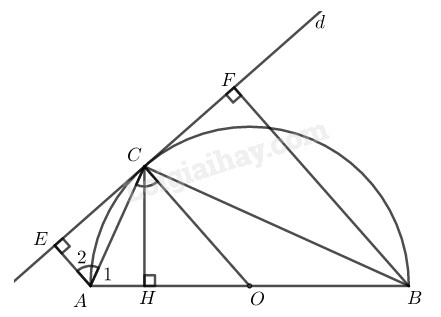
\(a)\) Ta có: \(OC ⊥d\) ( tính chất tiếp tuyến)
\(AE ⊥ d\;\; (gt)\)
\(BF ⊥ d \;\;(gt)\)
Suy ra: \(OC // AE // BF \;\;(*)\)
Mà \(OA = OB (=R)\)
Suy ra:\( CE = CF\) (tính chất đường thẳng song cách đều)
\(b)\) Ta có: \(AE // OC\) (theo \((*)\))
Suy ra: \(\widehat {OCA} = \widehat {EAC}\) ( hai góc sole trong) \((1)\)
Ta có: \(OA = OC (=R)\)
Suy ra: \(∆OAC\) cân tại \(O\) \( \Rightarrow \widehat {OCA} = \widehat {OAC}\) \((2)\)
Từ \((1)\) và \((2)\) suy ra: \(\widehat {EAC} = \widehat {OAC}\)
Vậy \(AC\) là tia phân giác của góc \(OAE\) hay \(AC\) là tia phân giác của góc \(BAE.\)
\(c)\) Tam giác \(ABC\) nội tiếp trong đường tròn \((O)\) có \(AB\) là đường kính nên \(\widehat {ACB} = 90^\circ \)
Tam giác \(ABC\) vuông tại \(C\) có \(CH ⊥ AB.\)
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
\(C{H^2} = HA.HB\;\; (3)\)
Xét hai tam giác \(ACH\) và \(ACE,\) ta có:
+) \(\widehat {AEC} = \widehat {AHC} = 90^\circ \)
+) \(CH = CE\) (tính chất đường phân giác)
+) \(AC\) chung
Suy ra: \(∆ACH = ∆ACE\) (cạnh huyền, cạnh góc vuông)
Suy ra: \(AH = AE\;\;(4)\)
Xét hai tam giác \(BCH\) và \(BEF,\) ta có:
+) \(\widehat {BHC} = \widehat {BFC} = 90^\circ \)
+) \(CH = CF (= CE)\)
+) \(BC \)chung
Suy ra: \(∆BCH = ∆BCF\) (cạnh huyền, cạnh góc vuông)
Suy ra: \(BH = BF \;\;(5)\)
Từ \((3),\) \((4)\) và \((5)\) suy ra: \(C{H^2} = AE.BF\)