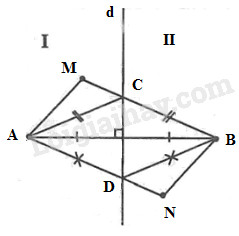
a) Nối \(MA, MB.\) Gọi \(C\) là giao điểm của MB với đường thẳng \(d,\) nối \(CA.\)
Ta có: \(MB = MC + CB\)
Mà \(CA = CB\) (tính chất đường trung trực)
Suy ra: \( MB = MC + CA\) (1)
Trong \(∆ MAC\) ta có:
\(MA < MC + CA\) (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra: \(MA < MB\)
b) Nối \(NA, NB.\) Gọi \(D\) là giao điểm của \(NA\) với đường thẳng \(d,\) nối \(DB.\)
Ta có: \(NA = ND + DB\)
Mà: \(DA = DB\) (tính chất đường trung trực)
Suy ra: \(NA = ND + DB \) (3)
Trong \(∆NDB\) ta có:
\(NB < ND + DB\) (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: \(NA > NB\)