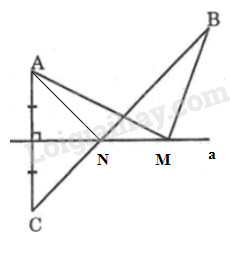
a) Gọi \(N\) là giao điểm của \(BC\) với đường thẳng \(a.\)
+) Nếu \(M \ne N\)
Nối \(MC\)
\(a\) là đường trung trực của \(AC\) mà \(M ∈ a\)
\( \Rightarrow MA = MC\) (tính chất đường trung trực) (1)
Trong \(∆MBC\) ta có:
\(BC < MB + MC\) (bất đẳng thức tam giác) (2)
Thay (1) vào (2) ta có: \(BC < MA + MB\)
+) Nếu \(M\) trùng với \(N,\) ta nối \(NA\)
\(NA = NC\) (tính chất đường trung trực)
Nên \(MA + MB = NA + NB\)\( = NC + NB = BC\)
Vậy: \(MA + MB ≥ BC\)
b) Theo chứng minh câu a ta có: Khi \(M\) trùng với \(N\) thì \(MA + MB = BC\) là nhỏ nhất.
Vậy \(M\) là giao điểm của \(BC\) với đường thẳng \(a\) thì \(MA + MB\) nhỏ nhất.