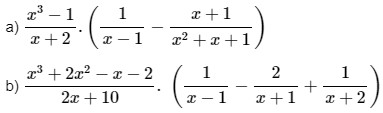Bài 7. Phép nhân các phân thức đại số

Bài 29

Làm tính nhân phân thức :

\(\eqalign{
& a)\;{{30{x^3}} \over {11{y^2}}}.{{121{y^5}} \over {25x}} \cr 
& b)\;{{24{y^5}} \over {7{x^2}}}.\left( { - {{21x} \over {12{y^3}}}} \right) \cr 
& c)\;\left( { - {{18{y^3}} \over {25{x^4}}}} \right).\left( { - {{15{x^2}} \over {9{y^3}}}} \right) \cr 
& d)\;{{4x + 8} \over {{{\left( {x - 10} \right)}^3}}}.{{2x - 20} \over {{{\left( {x + 2} \right)}^2}}} \cr 
& e)\;{{2{x^2} - 20x + 50} \over {3x + 3}}.{{{x^2} - 1} \over {4{{\left( {x - 5} \right)}^3}}} \cr} \)

Đề bài

Rút gọn biểu thức (chú ý dùng quy tắc đổi dấu để thấy nhân tử chung) : 

a) \(\displaystyle{{x + 3} \over {{x^2} - 4}}.{{8 - 12x + 6{x^2} - {x^3}} \over {9x + 27}}\)

b) \(\displaystyle{{6x - 3} \over {5{x^2} + x}}.{{25{x^2} + 10x + 1} \over {1 - 8{x^3}}}\)

c) \(\displaystyle{{3{x^2} - x} \over {{x^2} - 1}}.{{1 - {x^4}} \over {{{\left( {1 - 3x} \right)}^3}}}\)

Đề bài

Phân tích các tử thức và các mẫu thức (nếu cần thì dùng phương pháp thêm và bớt cùng một số hạng hoặc tách một số hạng thành hai số hạng) rồi rút gọn biểu thức :

a) \(\displaystyle{{x - 2} \over {x + 1}}.{{{x^2} - 2x - 3} \over {{x^2} - 5x + 6}}\)

b) \(\displaystyle{{x + 1} \over {{x^2} - 2x - 8}}.{{4 - x} \over {{x^2} + x}}\)

c) \(\displaystyle{{x + 2} \over {4x + 24}}.{{{x^2} - 36} \over {{x^2} + x - 2}}\)

Đề bài

Áp dụng tính chất phân phối của phép nhân đối với phép cộng để rút gọn biểu thức :

a) \(\displaystyle{{{x^3}} \over {x + 1975}}.{{2x + 1954} \over {x + 1}} \) \(\displaystyle + {{{x^3}} \over {x + 1975}}.{{21 - x} \over {x + 1}}\)

b) \(\displaystyle{{19x + 8} \over {x - 7}}.{{5x - 9} \over {x + 1945}} \) \(\displaystyle- {{19x + 8} \over {x - 7}}.{{4x - 2} \over {x + 1945}}\)

Đề bài

Tính tích \(x,\, y\) , biết rằng \(x\) và \(y\) thỏa mãn các đẳng thức sau (\(a,\, b\) là các hằng số) :

a) \(\displaystyle\left( {4{a^2} - 9} \right)x = 4a + 4\) với \(\displaystyle a ≠ \pm {3 \over 2}\) và \(\displaystyle\left( {3{a^3} + 3} \right)y = 6{a^2} + 9a\) với \(\displaystyle a ≠ − 1\).

b) \(\displaystyle\left( {2{a^3} - 2{b^3}} \right)x - 3b = 3a\) với \(\displaystyle a ≠ b\) và \(\displaystyle\left( {6a + 6b} \right)y = {\left( {a - b} \right)^2}\) với \(\displaystyle a ≠ − b\).

Chú ý rằng: \(\displaystyle{a^2} + ab + {b^2} = {a^2} + 2a.{b \over 2} + {{{b^2}} \over 4} + {{3{b^2}} \over 4} \) \(\displaystyle = {\left( {a + {b \over 2}} \right)^2} + {{3{b^2}} \over 4} \ge 0\).

Do đó nếu \(a ≠ 0\) hoặc \(b ≠ 0\) thì \(\displaystyle{a^2} + ab + {b^2} > 0\)

Đề bài

Rút gọn biểu thức :

a) \(\displaystyle{{{x^4} + 15x + 7} \over {2{x^3} + 2}}.{x \over {14{x^2} + 1}}.\) \(\displaystyle {{4{x^3} + 4} \over {{x^4} + 15x + 7}}\)

b) \(\displaystyle{{{x^7} + 3{x^2} + 2} \over {{x^3} - 1}}.{{3x} \over {x + 1}}.{{{x^2} + x + 1} \over {{x^7} + 3{x^2} + 2}}\) 

Đề bài

Đố: Đố em điền được một phân thức vào chỗ trống trong đẳng thức sau : 

\(\displaystyle{1 \over x}.{x \over {x + 1}}.{{x + 1} \over {x + 2}}.{{x + 2} \over {x + 3}}.{{x + 3} \over {x + 4}}\) \(\displaystyle.{{x + 4} \over {x + 5}}.{{x + 5} \over {x + 6}}.{{x + 6} \over {x + 7}}.{{x + 7} \over {x + 8}}.{{x + 8} \over {x + 9}}\) \(\displaystyle .{{x + 9} \over {x + 10}}.\;... = 1\)

Đề bài

Thực hiện các phép tính sau bằng hai cách : dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này : 

Đề bài

Thực hiện phép nhân : 

\(\displaystyle{1 \over {1 - x}}.{1 \over {1 + x}}.{1 \over {1 + {x^2}}}.{1 \over {1 + {x^4}}}.\) \(\displaystyle {1 \over {1 + {x^8}}}.{1 \over {1 + {x^{16}}}}\)