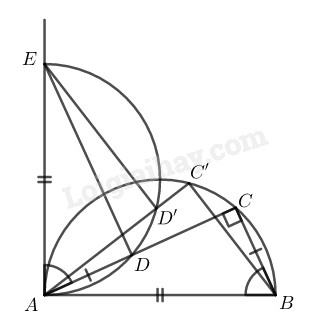
\(a)\) Chứng minh thuận
Nối \(DE.\) Xét \(∆ABC\) và \(∆AED:\)
\(AB = AE\;\; (gt)\)
\(AD = BC \;\;(gt)\)
\(\widehat {EAD} = \widehat {ABC}\) (hệ quả góc giữa tia tiếp tuyến và dây cung)
Suy ra: \(∆ABC = ∆EAD \;\;(c.g.c)\)
\( \Rightarrow \widehat {EAD} = \widehat {ACB}\)
Mà \(\widehat {ACB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \widehat {EDA} = {90^0}\)
Điểm \(C\) chuyển động trên nửa đường tròn đường kính \(AB\) thì điểm \(D\) luôn nhìn đoạn \(AE\) cố định dưới một góc bằng \(90^0\) nên điểm \(D\) nằm trên nửa đường tròn đường kính \(AE\) nằm trong nửa mặt phẳng bờ \(AE\) chứa nửa đường tròn đường kính \(AB.\)
Chứng minh đảo:
Trên nửa đường tròn đường kính \(AE\) lấy điểm \(D’\) bất kỳ, đường thẳng \(AD’\) cắt nửa đường tròn đường kính \(AB\) tại \(C’.\) Nối \(ED’, BC’.\)
Xét \(∆AD'E\) và \(∆BC'A:\)
\(\widehat {D'} = \widehat {C'} = {90^0}\) (các góc nội tiếp chắn nửa đường tròn)
\(AE = AB\;\; (gt)\)
\(\widehat {EAD} = \widehat {ABC'}\) (\(2\) góc cùng phụ \(\widehat {C'AB}\))
Suy ra: \(∆AD'E = ∆BC'A\) (cạnh huyền, góc nhọn)
\( \Rightarrow AD' = BC'\)
Vậy khi điểm \(C\) chạy trên nửa đường tròn đường kính \(AB\) thì quỹ tích điểm \(D\) là nửa đường tròn đường kính \(AE.\)
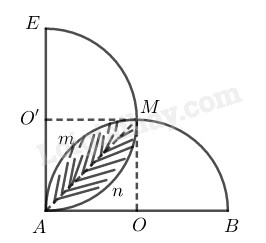
\(b)\) Gọi tâm hai nửa đường tròn đường kính \(AB\) và \(AE\) lần lượt là \(O\) và \(O’,\) giao điểm thứ hai của hai đường tròn là \(M\)
Ta có: \(OA = OM = O’A = O’M\) (vì \(AB = AE\))
Suy ra tứ giác \(AOMO’\) là hình thoi.
Ta lại có: \(\widehat A = {90^0}\) nên tứ giác \(AOMO’\) là hình vuông
Vậy tứ giác \(AOMO’\) là hình vuông
Diện tích phần chung của hai nửa hình tròn bằng diện tích hai quạt tròn có cung \(\overparen{AmM}\) trừ đi diện tích hình vuông
Diện tích hình quạt tròn \(AOM\) bằng:
\(\displaystyle {{\pi {{\left( \displaystyle {{{AB} \over 2}} \right)}^2}.90} \over {360}} = {{\pi A{B^2}} \over {16}}\)
Diện tích của hình vuông \(AOMO’\) bằng:
\(\displaystyle {\left( {{{AB} \over 2}} \right)^2} = {{A{B^2}} \over 4}\)
Diện tích phần chung bằng:
\(\displaystyle 2.{{\pi A{B^2}} \over {16}} - {{A{B^2}} \over 4} = {{\pi A{B^2}} \over 8} - {{2A{B^2}} \over 8}\)
\( =\displaystyle {{A{B^2}} \over 8}\left( {\pi - 2} \right)\) (đơn vị diện tích)