Bài 1 trang 43 SGK Giải tích 12
Lời giải
Bài Tập và lời giải
Đề bài
Động cơ nào sau đây không phải là động cơ nhiệt ?
A. Động cơ của máy bay phản lực.
B. Động cơ cùa xe máy Hon-đa.
C. Động cơ chạy máy phát điện của nhà máy thủy điện Sông Đà.
D. Động cơ chạy máy phát diện của nhà máy nhiệt điện.
Đề bài
Câu nào sau đây nói về hiệu suất của động cơ nhiệt?
A. Hiệu suất cho biết động cơ mạnh hay yếu.
B. Hiệu suất cho biết động cơ thực hiện công nhanh hay chậm.
C. Hiệu suất cho biết nhiệt lượng tảa ra khi 1kg nhiên liệu bị đốt cháy hoàn toàn trong động cơ.
D. Hiệu suất cho biết có bao nhiêu phần trăm nhiệt lượng do nhiên liệu bị đốt cháy tỏa ra được biến thành công có ích.
Đề bài
Một ôtô chạy 100km với lực kéo không đổi là 700N thì tiêu thụ hết 6 lít xăng. Tính hiệu suất của động cơ ô tô đó. Biết năng suất tỏa nhiệt của xăng là 4,6.107J/kg; khối lượng riêng của xăng là 700kg/m3.
Đề bài
Một máy bơm nước sau khi tiêu thụ hết 8kg dầu thì đưa được 700m3nước lên cao 8m. Tính hiệu suất máy bơm đó? Biết năng suất tỏa nhiệt của dầu dùng cho máy bơm này là 4,6.107 J/kg, khối lượng riêng của xăng là 700kg/m3.
Đề bài
Với 2 lít xăng, một xe máy có công suất là 6kW chuyển động với vận tốc 36km/h sẽ đi được bao nhiêu? Biết hiệu suất của động cơ là 25% ; năng suất tỏa nhiệt của xăng là 4,6.107 J/kg ; khối lượng riêng của xăng là 700kg/m3.
Đề bài
Động cơ của một máy bay có công suất 2.106w và hiệu suất 30%. Hỏi với 1 tấn xăng máy bay có thể bay được bao nhiêu lâu ? Năng suất tỏa nhiệt của xăng là 4,6.107J/kg
Đề bài
Tính hiệu suất của động cơ một ôtô biết rằng khi ôtô chuyển động với vận tốc 72km/h thì động cơ có công suất 20kW và tiêu thụ 20 lít xăng để chạy 200km.
Đề bài
Gọi H là hiệu suất động cơ nhiệt, A là công động cơ thực hiện được, Q là nhiệt lượng toàn phần do nhiên liệu bị đốt cháy tỏa ra, Q1 là nhiệt lượng có ích, Q2 là nhiệt lượng tỏa ra môi trường bên ngoài. Công thức tính hiệu suất nào sau đây là đúng?
A. \(H = {\dfrac{Q_1 - Q_2}{Q}}\)
B. \(H = \dfrac{Q_2 - Q_1}{Q}\)
C. \(H = \dfrac{Q - Q_2}{Q}\)
D. \(H = \dfrac{Q}{A}\)
Đề bài
Các kì của động cơ nổ bốn kì diễn ra theo thứ tự :
A. hút nhiên liện, đốt nhiên liệu, nén nhiên liệu, thoát khí
B. thoát khí, hút nhiên liệu, nén nhiên liệu, đốt nhiên liệu
C. hút nhiên liệu, nén nhiên liệu, thoát khí, đốt nhiên liệu
D. hút nhiên liệu, nén nhiên liệu, đốt nhiên liệu, thoát khí
Đề bài
Từ công thức \(H = \dfrac{A}{Q}\), ta có thể suy ra là đối với một xe ôtô chạy bằng động cơ nhiệt thì:
A. Công mà động cơ sinh ra tỉ lệ với khỏi lượng nhiên liệu bị đốt cháy
B. Công suất của động cơ tỉ lệ với khối lượng nhiẻn liện bị đốt cháy
C. Vận tốc của xe ti lệ với khôi lượng nhiẻn liệu bị đốt cháy
D. Quãng đường xe đi được tỉ lệ với khối lượng nhiên liệu bị đốt cháy
Đề bài
Người ta dùng một máy hơi nước hiệu suất 10% để đưa nước lên độ cao 9m. Sau 5 giờ máy bơm được 720m nước. Tính:
a) công suất có ích của máy ;
b) lượng than đá tiêu thụ. Biết nâng suất tòa nhiệt của than đá là 27.106J/kg
Đề bài
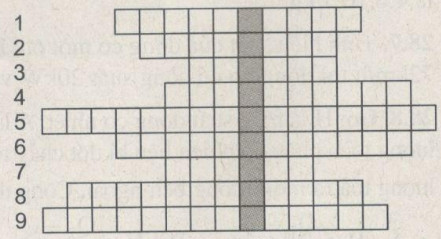
Ô chữ về nhiệt năng (H.28.1)
Hàng ngang
1. Tên hình thức truyền nhiệt trong chân không
2. Tên hình thức truyền nhiệt chủ yếu của chất rán
3. Tên hình thức truyền nhiệt chủ yếu của chất lỏng
4. Đại lượng nhiệt có cùng đơn vị của nâng lượng
5. Đại lượng cho biết khả năng tòa nhiét của nhiên liệu khi cháy
6. Khi đến trạng thái này thì nhiệt độ của các vật trao đổi nhiệt với nhau đều bằng nhau.
7. Tên của dạng năng lượng mà dễ dàng có thể chuyển hóa thành nhiệt năng.
8. Tên một cách làm thay đổi nhiệt năng
9. Đại lượng này có đơn vị là J/kg.K
Tên hàng dọc được tô sẫm:
Tên dạng năng lượng thường gặp nhất ở chương II.