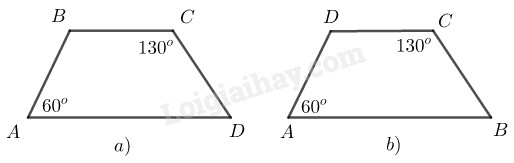
Hình thang \(ABCD\) ta có, \(\widehat A\) và \(\widehat C\) là hai góc đối
\(a)\) Trường hợp \(\widehat A\) và \(\widehat B\) là hai góc kề với cạnh bên.
\(⇒ AD // BC\)
\(\widehat A + \widehat B = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat B = {180^0} - \widehat A = {180^0} - {60^0} = {120^0}\)
\(\widehat C + \widehat D = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat D = {180^0} - \widehat C = {180^0} - {130^0} = {50^0}\)
\(b)\) Trường hợp \(\widehat A\) và \(\widehat D\) là hai góc kề với hai cạnh bên
\(⇒ AB // CD\)
\(\widehat A + \widehat D = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat D = {180^0} - \widehat A = {180^0} - {60^0} = {120^0}\)
\(\widehat B + \widehat C = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat B = {180^0} - \widehat C = {180^0} - {130^0} = {50^0}\)