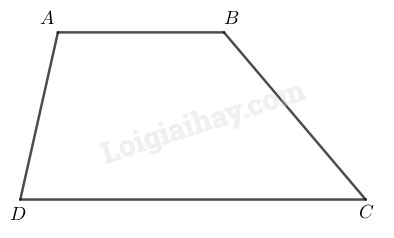
Xét hình thang \(ABCD\) có \(AB// CD\)
\( \widehat A\) và \(\widehat D\) là hai góc kề với cạnh bên.
\( \Rightarrow \widehat A + \widehat D = {180^0}\) (\(2\) góc trong cùng phía ) nên trong hai góc đó có nhiều nhất \(1\) góc nhọn và có nhiều nhất là \(1\) góc tù.
\(\widehat B\) và \(\widehat C\) là hai góc kề với cạnh bên
\( \Rightarrow \widehat B + \widehat C = {180^0}\) (\(2\) góc trong cùng phía) nên trong hai góc đó có nhiều nhất \(1\) góc nhọn và có nhiều nhất \(1\) góc tù.
Vậy bốn góc là : \(\widehat A,\widehat B,\widehat C,\widehat D\) có nhiều nhất là hai góc nhọn và nhiều nhất là hai góc tù.