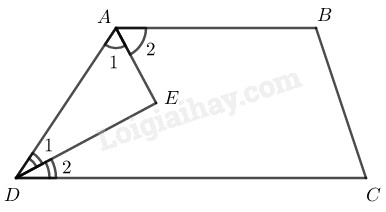
Giải sử hình thang \(ABCD\) có \(AB// CD\)
\(\eqalign{
& {\widehat A_1} = {\widehat A_2} = {1 \over 2}\widehat A(gt) \cr
& {\widehat D_1} = {\widehat D_2} = {1 \over 2}\widehat D(gt) \cr} \)
Mà \(\widehat A + \widehat D = {180^0}\) (hai góc trong cùng phía bù nhau)
Suy ra:
\({\widehat A_1} + {\widehat D_1} = \displaystyle {1 \over 2}(\widehat A + \widehat D )\)\(=\displaystyle{1 \over 2}.180^0= {90^0}\)
Trong \(∆ AED\) ta có :
\(\widehat {AED} + {\widehat A_1} + {\widehat D_1} = {180^0}\) (tổng ba góc trong tam giác)
\( \Rightarrow \widehat {AED} = {180^0} - \left( {{{\widehat A}_1} + {{\widehat D}_1}} \right) \)\(= {180^0} - {90^0} = {90^0}\)
Vậy \(AE ⊥ DE\)