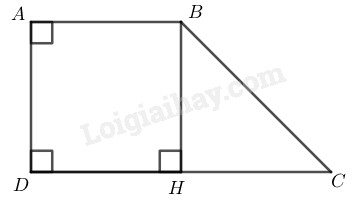
Kẻ \(BH ⊥ CD\)
Ta có: \(AD ⊥ CD\;\; (gt)\)
Suy ra: \(BH // AD.\)
Hình thang \(ABHD\) có hai cạnh bên song song
Nên \(HD = AB\) và \(BH = AD\)
\(AB = AD = 2cm\;\; (gt)\)
\(⇒ BH = HD = 2cm\)
\(CH = CD – HD \)\(=4− 2=2cm\)
Suy ra: \(∆ BHC\) vuông cân tại \(H\)
\(\eqalign{
& \Rightarrow \widehat B + \widehat C = {90^o} \cr
& \Rightarrow \widehat B = \widehat C = {90^o}:2 = {45^o} \cr} \)
Trong tứ giác \(ABCD\) có : \(\widehat B + \widehat C = {180^0}\) (hai góc trong cùng phía)
\(\Rightarrow \widehat B = {180^0} - \widehat C = {180^0} - {45^0} = {135^0}\)