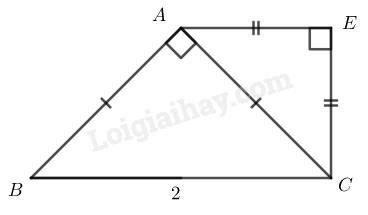
\(a)\) \(∆ ABC\) vuông cân tại \(A\)
\(\Rightarrow \widehat {ACB} = {45^0}\)
\(∆ EAC\) vuông cân tại \(E\)
\( \Rightarrow \widehat {EAC} = {45^0}\)
Suy ra: \(\widehat {EAC} = \widehat {ACB}\)
\(⇒ AE // BC\) (vì có cặp góc ở vị trí so le trong bằng nhau)
nên tứ giác \(AECB\) là hình thang có \(\widehat E = {90^0}\). Vậy \(AECB\) là hình thang vuông
\( b)\) \(\widehat E = \widehat {ECB} = {90^0},\widehat B = {45^0}\)
\(\widehat B + \widehat {EAB} = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat {EAB} = {180^0} - \widehat B\)\( = {180^0} - {45^0} = {135^0}\)
\(∆ ABC\) vuông tại \(A.\) Theo định lí Py-ta-go ta có:
\(A{B^2} + A{C^2} = B{C^2}\) mà \(AB= AC \;\;(gt)\)
\(\Rightarrow 2A{B^2} = B{C^2} = {2^2} = 4 \)
\( A{B^2} = 2 \Rightarrow AB = \sqrt 2 (cm) \)
\(\Rightarrow AC = \sqrt 2 (cm) \)
\(∆ AEC\) vuông tại \(E.\) Theo định lí Py-ta-go ta có:
\(E{A^2} + E{C^2} = A{C^2}\), mà \(EA = EC\;\;\; (gt)\)
\(\eqalign{
& \Rightarrow 2E{A^2} = A{C^2} = 2 \cr
& \Rightarrow E{A^2} = 1 \cr
& \Rightarrow EA = 1(cm) \Rightarrow EC = 1(cm) \cr} \)