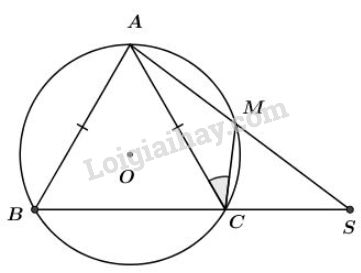
Xét đường tròn \((O)\), ta có:
\(\widehat{ASC}\) là góc có đỉnh ở ngoài đường tròn chắn cung \(MC\) và \(AB.\)
\(\Rightarrow \widehat{ASC} = \dfrac{sđ \overparen{AB}- sđ \overparen{MC}}{2}\) (1)
và \(\widehat {MCA}\) = \(\dfrac{sđ\overparen{AM}}{2}\) (2) (góc nội tiếp chắn cung \(\overparen{AM}\))
Theo giả thiết thì: \(AB = AC => \overparen{AB}=\overparen{AC}\) (hai dây bằng nhau căng hai cung bằng nhau).
\(\Rightarrow sđ\overparen{AB}-sđ\overparen{MC}=sđ\overparen{AC}-sđ\overparen{MC}=sđ\overparen{AM}\) (3)
Từ (1), (2), (3) suy ra: \(\widehat {ASC}=\widehat {MCA}.\) (đpcm)