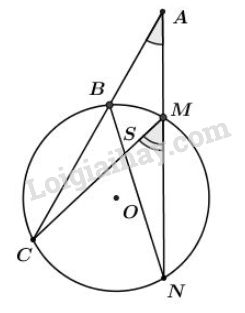
Xét đường tròn \((O)\) có:
+) \(\widehat A\) là góc có đỉnh nằm ngoài đường tròn \((O)\) chắn cung \(CN\) và \(BM\) \(\Rightarrow \widehat A = \dfrac{sđ\overparen{CN}-sđ\overparen{BM}}{2}\) (1)
+) \(\widehat {BSM}\) là góc có đỉnh nằm trong đường tròn \((O)\) chắn cung \(CN\) và \(BM\) \(\Rightarrow \widehat {BSM}=\dfrac{sđ\overparen{CN}+sđ\overparen{BM}}{2}\) (2)
Cộng (1) và (2) theo vế với vế:
\(\widehat{A}\)+\(\widehat {BSM}\)\(=\dfrac{2sđ\overparen{CN}+(sđ\overparen{BM}-sđ\overparen{BM)}}{2}=sđ \overparen{CN}\) (3)
Mà \(\widehat {CMN}\) là góc nội tiếp chắn cung \(CN\) \(\Rightarrow \widehat {CMN}=\dfrac{sđ\overparen{CN}}{2}\)
\(\Leftrightarrow\) \(2\widehat {CMN}=sđ\overparen{CN}\). (4)
Từ (3) và (4) ta được: \(\widehat A + \widehat {BSM} = 2\widehat {CMN}\) (đpcm).