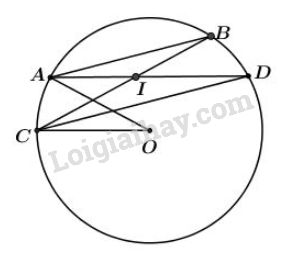
Theo giả thiết: \(\overparen{AC}=\overparen{BD}\) (vì \(AB // CD\)) (1)
Ta có: \(\widehat{AIC}\) là góc có đỉnh ở trong đường tròn chắn cung \(AC\) và cung \(BD\) \(\Rightarrow \widehat{AIC }= \dfrac{sđ\overparen{AC}+sđ\overparen{BD}}{2}\)
Theo (1) suy ra \(\widehat{AIC }=\dfrac{sđ\overparen{AC}+sđ\overparen{AC}}{2}\)\(=\dfrac{2.sđ\overparen{AC}}{2}= sđ\overparen{AC}\) (3)
Mà \(\widehat{AOC }= sđ\overparen{AC}\) (góc ở tâm chắn cung \(\overparen{AC}\)) (4)
Từ (3), (4), ta có \(\widehat{AOC } = \widehat{AIC }\) (đpcm).