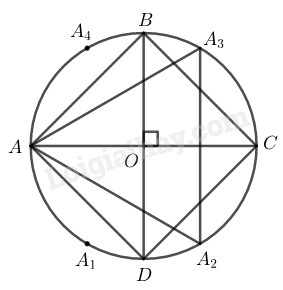
Cách vẽ:
− Vẽ đường tròn \((O; R)\)
− Kẻ \(2\) đường kính \(AC ⊥ BD\)
− Nối \(AB, BC, CD, DA\) ta được tứ giác \(ABCD\) là hình vuông nội tiếp trong đường tròn \((O; R)\)
− Từ \(A\) đặt liên tiếp các cung bằng nhau có dây tương ứng bằng bán kính \(R.\)
\(\overparen{{A}{A_1}},\) \(\overparen{{A_1}{A_2}},\) \(\overparen{{A_2}{C}},\) \(\overparen{{C}{A_3}},\) \(\overparen{{A_3}{A_4}}\)
Nối \({{A}{A_2}},\)\({{A_2}{A_3}},\)\({{A_3}{A}},\) ta có \(∆{{A}{A_2}{A_3}},\) là tam giác đều nhận \(O\) làm tâm.