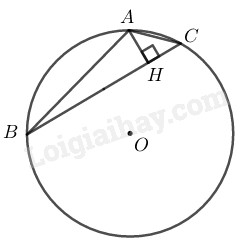
Dây \(AB\) bằng cạnh hình vuông nội tiếp đường tròn \((O; R)\) nên \(AB = R\sqrt 2 \)
và cung \(\overparen{AB}\) nhỏ có \(sđ \overparen{AB}=90^\circ\).
Dây \(BC\) bằng cạnh hình tam giác đều nội tiếp đường tròn \((O; R)\) nên \(BC = R\sqrt 3 \) và cung nhỏ \(\overparen{BC}\) có \(sđ \overparen{BC}= 120^\circ \).
\( \Rightarrow sđ \overparen{AC} = sđ \overparen{BC} - sđ \overparen{AB}\) \(=120^\circ - 90^\circ = 30^\circ \)
\( \Rightarrow \widehat {ABC} = \displaystyle {1 \over 2} sđ \overparen{AC}=15^\circ\) (tính chất góc nội tiếp)
Trong \(∆AHB\) có \(\widehat {AHB} = 90^\circ \)
\( \Rightarrow AH = AB.\sin \widehat {ABH} \)\(= R\sqrt 2 .\sin 15^\circ \approx 0,36R\)
Trong \(∆AHC\) có \(\widehat {AHC} = 90^\circ \)
\(\widehat {ACB} = \displaystyle{1 \over 2}\) sđ \(\overparen{AB}=45^\circ\) (tính chất góc nội tiếp)
\(AC =\displaystyle {{AH} \over {\sin \widehat {ACH}}} \)\(=\displaystyle {{AH} \over {\sin 45^\circ }} \approx {{0,36R} \over {\sin 45^\circ }} \approx 0,51R\)