Bài 1: Cạnh bên của tam giác cân đã cho không thể bằng 4,
vì \(4 + 4 < 9,\) trái với bất đảng thức tam giác nên cạnh bên phải là 9,
vì \(9 + 9 > 4.\) Do đó chu vi tam giác cân là \(2.9 + 4 = 22\) (cm).
Bài 2:
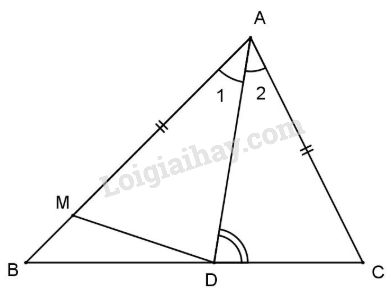
a) Xét \(\Delta A{\rm{D}}M\) và \(\Delta A{\rm{D}}C\) có:
+) AD cạnh chung
+) \({\widehat A_1} = {\widehat A_2}\) (gt);
+) \(AM = AC\) (gt).
Do đó \(\Delta A{\rm{D}}M = \Delta A{\rm{D}}C\) (c.g.c)
b) Vì \(AB > AC\) (gt) \( \Rightarrow \widehat B < \widehat C\).
Xét \(\Delta A{\rm{D}}B\) ta có \(\widehat {A{\rm{D}}C} + \widehat C + {\widehat A_2} = {180^0}.\)
Tương tự \(\Delta A{\rm{D}}C\) ta có \(\widehat {A{\rm{D}}C} + \widehat C + {\widehat A_2} = {180^0},\)
mà \({\widehat A_1} = {\widehat A_2}\) (gt); \(\widehat B < \widehat C\) (cmt)
\( \Rightarrow \widehat {ADB} = \widehat {ADC}\) (cmt).
Bài 3:
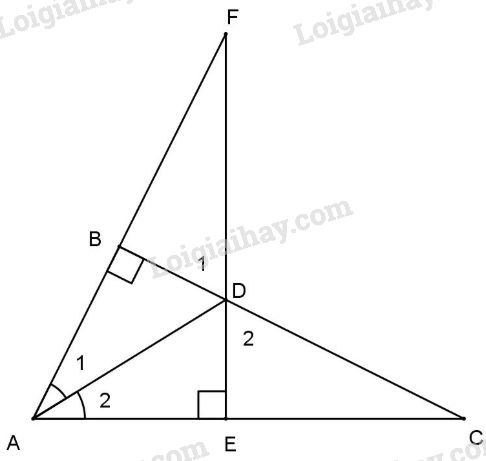
a) Xét hai tam giác vuông ABD và AED có :
+) AD cạnh chung;
+) \({\widehat A_1} = {\widehat A_2}\) (gt).
Do đó \(\Delta AB{\rm{D}} = \Delta A{\rm{ED}}\) (ch.gn)
\( \Rightarrow B{\rm{D}} = DE\) (cạnh tương ứng).
b) Xét tam giác vuông DEC ta có \(DE < DC\) (cgv<ch), mà DE = DB (cmt)
\( \Rightarrow C{\rm{D}} > DB\) .
c) Xét hai tam giác vuông DBF và DEC có:
+) \({\widehat D_1} = {\widehat D_2}\) (đối đỉnh);
+) \(DB = DE\) (cmt).
Do đó \(\Delta DBF = \Delta DEC\) (g.c.g)
\( \Rightarrow BF = EC\)
Lại có \(BA = E{\rm{A}}\) (cmt)
\( \Rightarrow BF + BA = EC + E{\rm{A}}\)
hay \(AF = AC.\)
Xét \(\Delta A{\rm{D}}F\) và \(\Delta A{\rm{D}}C\) có:
+) AD cạnh chung;
+) \({\widehat A_1} = {\widehat A_2}\) (gt);+) AF = AC (cmt)
\(\Delta A{\rm{D}}F = \Delta A{\rm{D}}C\) (c.g.c).
d) Ta có vế trái: \(BA + BC = A{\rm{E}} + B{\rm{D}} + DC\) (vì \(BA = A{\rm{E}}\) cmt).
Vế phải: \(DE + AC = DB + A{\rm{E}} + EC\) (vì DE = DB theo cmt).
Trong tam giác vuông DEC ta có \(DC > EC\) (ch-cgv).
Vậy \(A{\rm{E}} + B{\rm{D}} + DC > DB + A{\rm{E}} + EC\) hay \(BA + BC > DE + AC.\)