Bài 1: Ta có \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng ba góc trong tam giác)
\(\eqalign{ & \Rightarrow \widehat C = {180^0} - (\widehat B + \widehat A) \cr&\Rightarrow \widehat C = {180^0} - ({65^0} + {55^0}) \cr & \Rightarrow \widehat C = {180^0} - {120^0} = {60^0}. \cr} \)
Do đó \(\widehat B > \widehat C > \widehat A\) (\({65^0} > {60^0} > {55^0}\))
\( \Rightarrow AC > AB > BC.\)
(quan hệ cạnh và góc đối diện)
Bài 2:
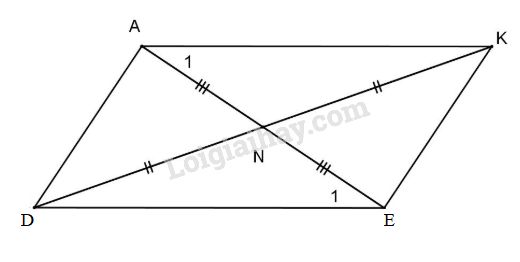
a) \(\Delta A{\rm{D}}E\) vuông tại A
Ta có \(D{E^2} = D{A^2} + E{{\rm{A}}^2}\) (định lý Pytago)
\(\eqalign{ & \Leftrightarrow D{E^2} = {8^2} + {15^2} \cr & \Leftrightarrow D{E^2} = 289 \cr & \Rightarrow DE = 17cm. \cr} \)
b) Xét \(\Delta AN{\rm{D}}\) và \(\Delta ENK.\)
Có \(AN = A{\rm{E}}\) (gt);
\(DN = KN\) (gt)
\(\widehat {AN{\rm{D}}} = \widehat {ENK}\) (đối đỉnh).
Do đó \(\Delta AN{\rm{D}} = \Delta ENK\) (c.g.c)
\( \Rightarrow A{\rm{D}} = EK\) (cạnh tương ứng).
c) Chứng minh tương tự ta có \(\Delta ANK = \Delta EN{\rm{D}}\) (c.g.c) \( \Rightarrow {\widehat A_1} = {\widehat E_1}\) (góc tương ứng)
\( \Rightarrow AK\) // DE (cắt – góc so le trong bằng nhau).
d) Xét \(\Delta A{\rm{D}}K\) theo bất đẳng thức tam giác ta có \(A{\rm{D}} + AK > DK.\)
\(AD + DE > 2DN\)(đpcm).