Nét đặc trưng của dòng sông Hương khi chảy vào thành phố trong bút kí Ai đặt tên cho dòng sông?

Hãy chứng minh khẳng định trên.

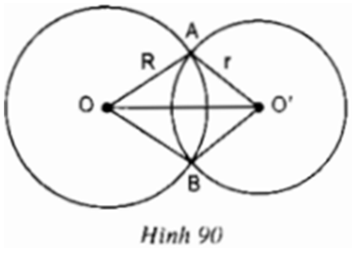
Hãy chứng minh các khẳng định trên.

(Tức là chứng minh:

Nếu hai đường tròn (O) và (O') tiếp xúc ngoài thì \(OO'=R+r.\)

Nếu hai đường tròn (O) và (O') tiếp xúc trong thì \(OO'=R-r.\))

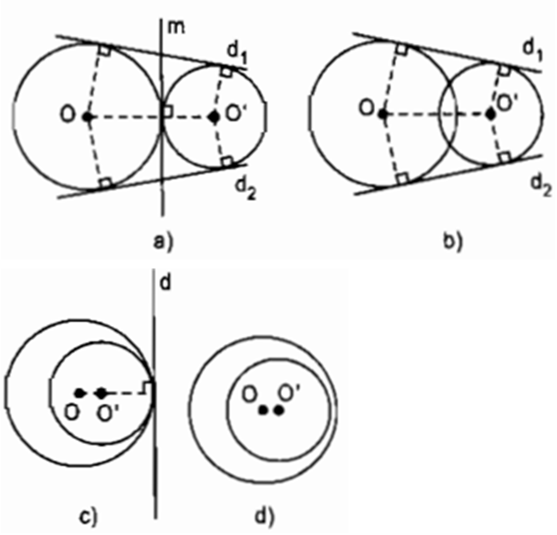
Quan sát các hình 97a, b, c, d trên hình nào có vẽ tiếp tuyến chung của hai đường tròn ? Đọc tên các tiếp tuyến chung đó.

Điền vào các ô trống trong bảng, biết rằng hai đường tròn \((O;R)\) và \((O';r)\) có \(OO'=d,\,\, R>r\)

Cho đường tròn tâm \(O\) bán kính \(OA\) và đường tròn đường kính \(OA\).

a) Hãy xác định vị trí tương đối của hai đường tròn.

b) Dây \(AD\) của đường tròn lớn cắt đường tròn nhỏ ở \(C\). Chứng minh rằng \(AC=CD\).

Cho hai đường tròn đồng tâm \(O\). Dây \(AB\) của đường tròn lớn cắt đường tròn nhỏ ở \(C\) và \(D\). Chứng minh rằng \(AC=BD\). 

Điền các từ thích hợp vào chỗ trống (...): 

a) Tâm của các đường tròn có bán kính \(1cm\) tiếp xúc ngoài với đường tròn \((O;\ 3cm)\) nằm trên ...

b) Tâm của các đường tròn có bán kính \(1cm\) tiếp xúc trong với đường tròn \((O;\ 3cm)\) nằm trên ...

Cho hai đường tròn \((O)\) và \((O')\) tiếp xúc ngoài tại \(A\). Kẻ tiếp tuyến chung ngoài \(BC\), \(B\in (O),C\in (O').\) Tiếp tuyến chung trong tại \(A\) cắt tiếp tuyến chung ngoài \(BC\) ở \(I\).

a) Chứng minh rằng \(\widehat{BAC}=90^{\circ}\).

b) Tính số đo góc \(OIO'\). 

c) Tính độ dài \(BC\), biết \(OA=9cm,\ O'A=4cm.\)

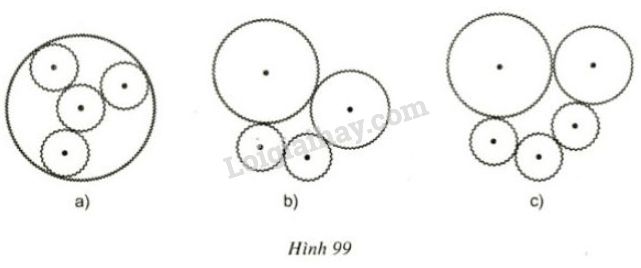
Trên các hình 99a, 99b, 99c, các bánh xe tròn có răng cưa được khớp với nhau. Trên hình nào hệ thống bánh răng chuyển động được? Trên hình nào hệ thống bánh răng không chuyển động được?

Cho nửa đường tròn tâm O, đường kính AB. Trên cùng nửa mặt phẳng bờ là AB, vẽ nửa đường tròn tâm O’ đường kính OA. Vẽ dây cung AC của (O) cắt nửa đường tròn (O’) tại D. Chứng minh:

a. Đường tròn (O) và (O’) tiếp xúc tại A.

b. O’D và OC song song với nhau.

Cho đoạn thẳng \(OO’ = 13cm\). Dựng đường tròn (O; 12cm) và (O’; 5cm)

a. Chứng tỏ (O) và (O’) cắt nhau tại hai điểm phân biệt A và B.

b. Vẽ đường kính AC của (O) và AD của (O’). Chứng minh ba điểm C, B, D thẳng hàng.

Cho đoạn thẳng OO’ và điểm A nằm giữa hai điểm O và O’.

Vẽ đường tròn (O; OA) và đường tròn (O’; O’A). Qua A vẽ đường thẳng cắt (O) tại B và cắt (O’) tại C.

a. Chứng minh (O) và (O’) tiếp xúc nhau.

b. Vẽ đường kính BD của (O) và CE của (O’). Chứng minh D, A, E thẳng hàng.

Cho tam giác ABC vuông tại A có \(AB = 6cm, AC = 8cm\), đường cao AH. Đường tròn (O) đường kính AH cắt AB tại D, đường tròn (O’) đường kính CH cắt AC tại E.

a. Chứng minh (O) và (O’) cắt nhau tại hai điểm phân biệt.

b. Chứng minh đường thẳng DE là tiếp tuyến của (O’).

Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Đường thẳng OO’ cắt (O) và (O’) lần lượt tại B và C (khác A). Gọi DE là tiếp tuyến chung ngoài của (O) và (O’). Trong đó, \(D ∈ (O), E ∈ (O’)\). Gọi H là giao điểm của hai đường thẳng BD và CE. Chứng minh rằng :

a. \(\widehat {DHE} = 90^\circ \)

b. HA là tiếp tuyến chung của hai đường tròn (O) và (O’).

Cho đường tròn (O; R) và (O’; R’) tiếp xúc ngoài nhau tại A. Một tiếp tuyến chung ngoài TT’ \((T ∈ (O), T’ ∈ (O’))\) cắt tiếp tuyến qua A tại B.

a. Chứng tỏ \(BT = BT’\)

b. Chứng minh ∆OBO’ vuông và \(TT' = 2\sqrt {RR'} \)

Hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B. Gọi AC và AD lần lượt là các đường kính của (O) và (O’).

a. Chứng minh ba điểm C, B, D thẳng hàng.

b. Qua A vẽ cát tuyến cắt (O) tại M, cắt (O’) tại N (M, N khác A). Chứng minh rằng: \(MN ≤ CD.\)

Cho hình bình hành ABCD (\(AB > AD\)). Vẽ đường tròn tâm A bán kính AD, đường tròn (A) cắt AB tại E. Vẽ đường tròn tâm B bán kính BE, đường tròn (B) cắt đường thẳng DE tại F. Chứng minh đường tròn (A; AD) và (B; BE) tiếp xúc với nhau và ba điểm F, B, C thẳng hàng.

Cho đường tròn (O) đường kính BC. Một dây AD vuông góc với BC tại H. Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I) và (K) lần lượt là các đường tròn ngoại tiếp các tam giác HBE và HCF.

a. Xác định vị trí tương đối của đường tròn (I) và (O); (K) và (O); (I) và (K).

b. Chứng minh tứ giác AEHF là hình chữ nhật.

Cho đường tròn tâm K có đường kính BC. Gọi D là trung điểm của KC và I là tâm của đường tròn có đường kính BD.

a. Chứng tỏ hai đường tròn (K) và (I) tiếp xúc trong với nhau.

b. Qua B vẽ đường thẳng (không trùng với BC) cắt (K) và (I) lần lượt tại A và E. Chứng tỏ KA // IE và \({{CA} \over {DE}}\) không đổi.