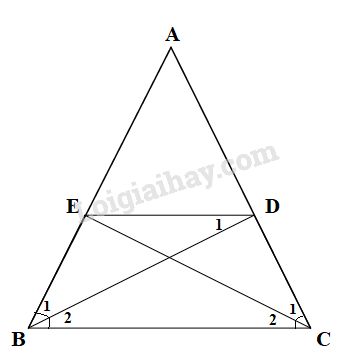
Bài 16 trang 75 SGK Toán 8 tập 1
Lời giải
Bài Tập và lời giải
II. Em suy nghĩ - Bài 4: Lễ độ
Giải bài tập 1, 2, 3 trang 12, 13 sách bài tập tình huống Giáo dục công dân 6. Câu thần chú mà ông già mách cho chú bé là gì?
I. Em đọc truyện "Lời nói có phép lạ"
Em đọc truyện "Lời nói có phép lạ" trang 11, 12 sách Bài tập tình huống Giáo dục công dân 6. Cụ già cầm tay cậu bé, hỏi - Làm sao cháu khóc ? Cháu có điều gì bực tức phải không ? ....
I. Em đọc truyện "Lạc đàn"
Em đọc truyện "Lạc đàn" trang 13, 14 sách Bài tập tình huống Giáo dục công dân 6. Nhà Kiến ở ven sông, sâu trong một hẻm đá, thật đông và vui ....
II. Em suy nghĩ - Bài 5: Tôn trọng kỉ luật
Giải bài tập 1, 2, 3 trang 14, 15 sách bài tập tình huống Giáo dục công dân 6. Đàn kiến đi kiếm ăn trong truyện được tả như thế nào?