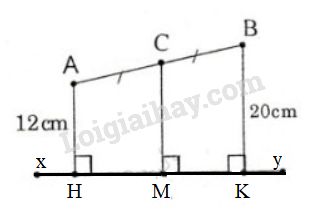
Bài 24 trang 80 SGK Toán 8 tập 1
Lời giải
Bài Tập và lời giải
III. Bài học rút ra - Bài 10: Tích cực, tự giác trong hoạt động tập thể và hoạt động xã hội
Em hãy rút ra bài học về đạo đức, ý thức công dân và ghi vào vở
I. Em đọc truyện "Câu chuyện trực nhật"
Em đọc truyện "Câu chuyện trực nhật" trang 25, 26, 27 sách Bài tập tình huống Giáo dục công dân 6. Buổi họp lớp diễn ra hơi nặng nề. Cô giáo Lan nhắc ....
I. Em đọc truyện "Câu chuyện điểm 10"
Em đọc truyện "Câu chuyện điểm 10" trang 28, 29, 30 sách Bài tập tình huống Giáo dục công dân 6. Hôm nay, sau giờ học Toán, khi cả lớp 7A đã túa ra về như một bầy ong vỡ tổ thì Giáng Hương tay vẫn ôm cặp ....
II. Em suy nghĩ - Bài 11: Mục đích học tập của học sinh
Giải bài tập 1, 2, 3 trang 30 sách bài tập tình huống Giáo dục công dân 6. Sau khi lên bảng chữa bài tập, cô giáo cho Giáng Hương điểm 10, Giáng Hương có phấn khởi không? Vì sao?