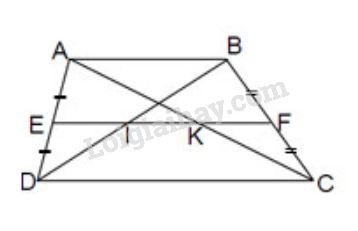
Bài 28 trang 80 SGK Toán 8 tập 1
Lời giải
Bài Tập và lời giải
II. Em suy nghĩ - Bài 11: Mục đích học tập của học sinh
Giải bài tập 1, 2, 3 trang 30 sách bài tập tình huống Giáo dục công dân 6. Sau khi lên bảng chữa bài tập, cô giáo cho Giáng Hương điểm 10, Giáng Hương có phấn khởi không? Vì sao?
I. Em đọc truyện
Em đọc truyện "Câu chuyện điểm 10" trang 28, 29, 30 sách Bài tập tình huống Giáo dục công dân 6. Hôm nay, sau giờ học Toán, khi cả lớp 7A đã túa ra về như một bầy ong vỡ tổ thì Giáng Hương tay vẫn ôm cặp ....
I. Em đọc các tình huống - Bài 12: Công ước Liên hợp quốc về quyền trẻ em
Em đọc các tình huống - Bài 12: Công ước Liên hợp quốc về quyền trẻ em trang 30, 31 sách Bài tập tình huống Giáo dục công dân 6. Cháu nội của bà Ngoan ở Trà Vinh tên là Nguyễn Nhật Trường, sinh năm 1986, bị xích chân khóa vào cầu thang ....
II. Em suy nghĩ - Bài 12: Công ước Liên hợp quốc về quyền trẻ em
Giải bài tập 1, 2, 3, 4 trang 31 sách bài tập tình huống Giáo dục công dân 6. Hình phạt của bà Ngoan đối với cháu (Trường) có đúng không? Vì sao?