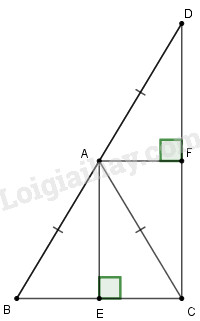
Vì \(∆ABC\) cân tại \(A,\) có \(A{\rm{E}} \bot BC\left( {gt} \right)\)
Hay \(AE\) là đường cao, suy ra \(AE\) cũng là đường phân giác của \(\widehat {BAC}\)
\( \Rightarrow \widehat {EAC} = \dfrac{1}{2}\widehat {BAC}\)
Từ gt suy ra: \(AD=AC=AB\) nên \(∆ADC\) cân tại \(A.\)
Vì \(∆ADC\) cân tại \(A,\) có \({\rm{AF}} \bot {\rm{DC}}\left( {gt} \right)\)
Hay\(AF\) là đường cao, suy ra \(AF\) cũng là đường phân giác của \(\widehat {CA{\rm{D}}}\)
\( \Rightarrow \widehat {FAC} = \dfrac{1}{2}\widehat {DAC}\)
Mà \(\widehat {BAC}\) và \(\widehat {CA{\rm{D}}}\) là hai góc kề bù.
Nên \(\Rightarrow \widehat {EAC} + \widehat {FAC} \)\(= \dfrac{1}{2}\left( {\widehat {BAC} + \widehat {DAC}} \right) \)\(= \dfrac{1}{2}.180^\circ = 90^\circ \)
Hay \(\widehat {EAF} = 90^\circ \)
Suy ra: \(A{\rm{E}} \bot {\rm{AF}}\)