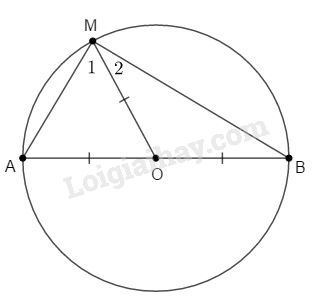
Nối \(OM\), ta có:
\(OA = OM\) (bằng bán kính đường tròn tâm \(O\))
\( \Rightarrow ∆OAM\) cân tại \(O\).
\( \Rightarrow \widehat A = \widehat {{M_1}}\) (tính chất tam giác cân) (1)
\(OM = OB\) (bằng bán kính đường tròn tâm \(O\))
\( \Rightarrow ∆OBM\) cân tại \(O\).
\( \Rightarrow \widehat {{M_2}} = \widehat B\) (tính chất tam giác cân) (2)
Áp dụng định lí tổng các góc của một tam giác vào \(∆AMB\), ta có:
\(\widehat A + \widehat {AMB} + \widehat B = 180^\circ \)
\( \Rightarrow \widehat A + \widehat {{M_1}} + \widehat {{M_2}} + \widehat B = 180^\circ \) (3)
Từ (1), (2) và (3) suy ra:
\(2.\left( {\widehat {{M_1}} + \widehat {{M_2}}} \right) = 180^\circ \)
\( \Rightarrow \widehat {{M_1}} + \widehat {{M_2}} =180^o:2= 90^\circ \) hay \(\widehat {AMB} = 90^\circ \)