Đề kiểm 15 phút - Đề số 1 - Bài 10 - Chương 3 -Hình học 9

Tính diện tích hình tròn nội tiếp một tam giác đều có cạnh là a.

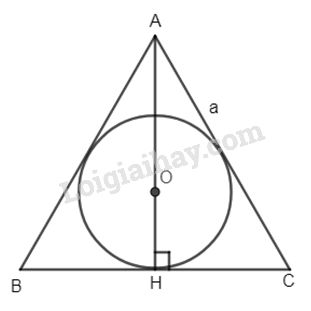
Gọi AH là đường cao.

Ta đã biết : Tâm của đường tròn nội tiếp tam giác đều trùng với trọng tâm tam giác.

Ta có: \(AH = \dfrac{{a\sqrt 3 }}{2}\).

Vì O là trọng tâmm tam giác nên

 \(OH = \dfrac{1}{3}AH = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}\)

Vậy

\(S_{\text{ hình tròn }}=\pi .{R^2} = \pi {\left( {\dfrac{{a.\sqrt 3 }}{6}} \right)^2} \)\(\,= \dfrac{{\pi {a^2}}}{{12}}.\)