Đề kiểm tra 15 phút - Đề số 5 - Bài 2 - Chương 3 - Hình học 9

Cho hai đường tròn đồng tâm (O; R) và (O; R’). Lấy điểm P trên (O; R) kẻ hai tia Px và Py không đi qua O và cắt hai đường tròn lần lượt tại A, B, C ( A, B \( \in \) ( O; R’)) và D, E, F ( E, D \( \in \) (O; R’)). Biết rằng AB < DE. Chứng minh rằng: \(\overparen{ PC}<\overparen{PF}\)

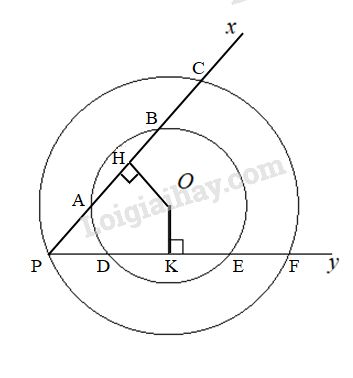
Kẻ \(OH  \bot  AB\) tại H và \(OK  \bot  DE\) tại K.

Ta có: \(AB < DE\) (gt)

\( \Rightarrow  OH > OK\) (định lí liên hệ giữa dây và khoảng cách đến tâm)

Trong đường tròn (O; R) có \(OH > OK\)

\( \Rightarrow  PC < PF\). Do đó \(\overparen{ PC}<\overparen{PF}\)