Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 3 - Hình học 9

Cho  đường tròn (O) dây cung AB. Tiếp tuyến của (O) tại A và B cắt nhau tại M. Biết \(\widehat {AMB} = 50^\circ \).

a) Tính số đo cung AB.

b) Trên nửa mặt phẳng bờ OB ( không chứa điểm A), kẻ đườngthẳng d qua O và song song với BM, d cắt (O) tại D. Tính số đo cung AD.

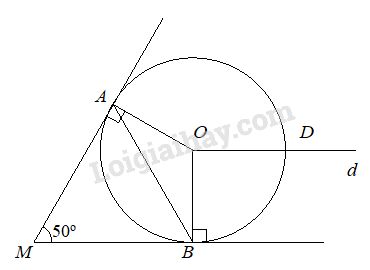
a) MA, MB là hai tiếp tuyến của (O) nên MA \( \bot \) OA và MB \( \bot \) OB.

Xét tứgiác AOBM có:

\(\widehat {AOB} = 360^\circ  - (\widehat {MAO} + \widehat {MBO} + \widehat {AMB}) \)\(\;= 360^\circ  - (90^\circ  + 90^\circ  + 50^\circ ) = 130^\circ \).

\(sd \overparen {AB}=sd\overparen{AOB}=130^o\)

b) Ta có: \(sd\overparen {ADB} = 360^o − \overparen {AB} = 360^o − 130^o\)\(\;= 230^o\)

Mặt khác OD // BM mà BM \( \bot \) OB \(\Rightarrow\) OD \( \bot \) OB

hay \(sd\overparen{AD} = sd\overparen{ADB }– sd\overparen{BD} \)\(\,= 230^o− 90^o=140^o\)