Đề kiểm 15 phút - Đề số 7 - Bài 4 - Chương 3 - Hình học 9

Từ một điểm P ở ngoài đường tròn (O), kẻ hai tiếp tuyến PA, PB đến đường tròn. Trên cung nhỏ AB lấy điểm C bất kì, kẻ các đường vuông góc CD, CE, CF lần lượt xuống các đường thẳng AB, BP, PA. Chứng minh rằng : \(\widehat {DCF} = \widehat {DCE}\) và \(\widehat {DFC} = \widehat {CDE}\).

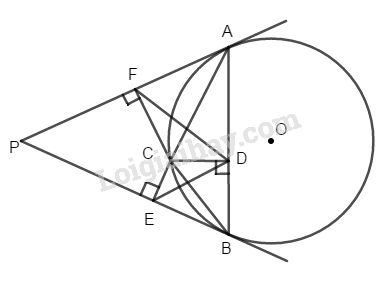
Ta có E và D nằm trên đường tròn đường kính BC, F và D nằm trên đường tròn đường kính AC.

Do đó \(\widehat {DCF} + \widehat {PAB} = \widehat {DCE} + \widehat {PBA} = 2v\)

Trong đó \(\widehat {PAB} = \widehat {PBA}\) ( góc giữa tiếp tuyến và một dây cùng chắn cung nhỏ AB).

Vậy \(\widehat {DCF} = \widehat {DCE}\).

Trong đường tròn (O), ta có : \(\widehat {CBE} = \widehat {CAB}\) (góc giữa tiếp tuyến và một dây và góc nội tiếp cùng chắn cung CB).

Trong đường tròn đường kính BC, ta có : \(\widehat {CBE} = \widehat {CDE}\) ( góc nội tiếp cùng chắn cung CE).

Trong đường tròn đường kính CA, ta có : \(\widehat {CAB} = \widehat {DFC}\) ( góc nội tiếp cùng chắn cung CD).

Vậy \(\widehat {DFC} = \widehat {CDE}\).