Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 3 - Hình học 9

Cho hai đường tròn (O) và (O') cắt nhau tại hai điểm phân biệt A và B. Biết rằng hai cung nhỏ AB của hai đường tròn này có số đo (độ) bằng nhau. Chứng minh rằng hai đường tròn (O) và (O') bằng nhau.

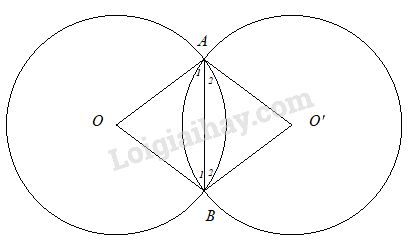
Ta có: Hai cung nhỏ AB của hai đường tròn này có số đo (độ) bằng nhau \( \Rightarrow \widehat {AOB} = \widehat {AO'B}\)

Mặt khác các tam giác AOB và AO'B có hai góc ở đỉnh bằng nhau nên bốn góc ở đáy cũng bằng nhau : \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{B_1}} = \widehat {{B_2}}\)

Do đó \(∆AOB = ∆AO'B\) (c.g.c) \(\Rightarrow  OA = O'A\)

Chứng tỏ hai đường tròn (O) và (O’) bằng nhau.