Đề kiểm 15 phút - Đề số 10 - Bài 7 - Chương 3 - Hình học 9

Cho tam giác ABC nội tiếp trong đường tròn (O). Từ một điểm bất kì trên đường tròn hạ các đường vuông góc xuống các cạnh. Chứng minh rằng chân ba đường vuông góc này thẳng hàng (đường thẳng Sim-Sơn).

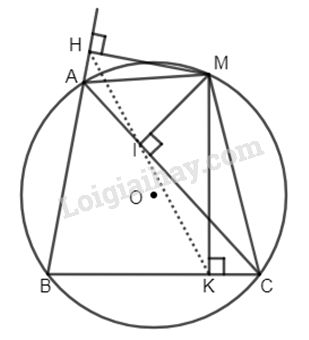
Gọi chân các đường vuông góc hạ từ M lần lượt xuống các cạnh AB, BC, CA là H, K, I.

Ta có tứ giác AHMI nội tiếp ( vì có \(\widehat {AHM} + \widehat {AIM} = 180^\circ \))

\( \Rightarrow \widehat {HAM} = \widehat {HIM}\)           (1)    ( góc nội tiếp cung chắn MH)

Tương tự tứ giác CKIM nội tiếp ( vì \(\widehat {CKM} + \widehat {CIM} = 90^\circ \))

\( \Rightarrow \widehat {MIK} + \widehat {MCK} = 180^\circ \)                       (2)

Mặt khác ABCM nội tiếp (O) nên \(\widehat {HAM} = \widehat {MCK}\)

Suy ra \(\widehat {HIM} = \widehat {MCK}\)

Do đó \(\widehat {MIK} + \widehat {HIM} = 180^\circ \)

\(\Rightarrow H, I, K\) thẳng hàng.

Trường hợp M thuộc các cung còn lại chứng minh tương tự.