Đề kiểm 15 phút - Đề số 1 - Bài 8 - Chương 3 - Hình học 9

Cho đường tròn (O; R). Vẽ hình vuông ABCD nội tiếp và tính cạnh của hình vuông theo R.

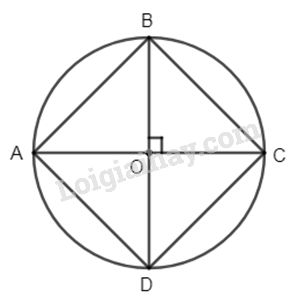
Thật vậy : các tam giác vuông AOB, BOC, COD, DOA bằng nhau nên \(AB = BC = CD =DA\).

Do đó ABCD là hình thoi.

Mặt khác \(\widehat {ABC} = 90^\circ \) (AC là đường kính) nên hình thoi ABCD là hình vuông.

Xét tam giác vuông AOB, ta có : \(AB = \sqrt {A{O^2} + B{O^2}}  = \sqrt {2{R^2}}  = R\sqrt 2 \)

Vậy cạnh của hình vuông nội tiếp đường tròn (O; R) là \(R\sqrt 2 \).